In my last article, we talked about Depth First Search (DFS) Algorithm and used it, in order to find the solution to a Sudoku puzzle. Today, we'll talk about another search algorithm called Breadth-First Search (BFS). After that, we will implement this algorithm in order to find a solution to the Maze problem.
Search Algorithms are used in order to find a solution to problems that can be modeled as a graph. If you do not know what a graph is please read the related article. Every node of a graph is an instance of the problem. Each search algorithm starts from a node (initial instance — state) and extends the node, creating new nodes (new instances of the problem) by applying a legal action of the problem. The whole process is stopped when the algorithm finds a solution (success — final state) or can not create new nodes (failure). Some of the most popular search algorithms are Depth First Search (DFS), Breadth-First Search (BFS), Greedy Algorithm, Uniform Cost Search (UCS), A*, etc. In this article are going to talk about Breadth-First Search (BFS) algorithm.
Also Read: A guide on how to implement the Graph data structure in Python
Breadth-First Search is a “blind” algorithm. It's called “blind” because this algorithm doesn't care about the cost between vertices on the graph. The algorithm starts from a root node (which is the initial state of the problem) and explores all nodes at the present level prior to moving on to the nodes at the next level. If the algorithm finds a solution, returns it and stops the search, otherwise extends the node and continues the search process. Breadth-First Search is “complete”, which means that the algorithm always returns a solution if exists. More specifically, the algorithm returns the solution that is closest to the root, so for problems that the transition from one node to its children nodes costs one, the BFS algorithm returns the best solution. In addition, in order to explore the nodes level by level, it uses a queue data structure, so new nodes are added at the end of the queue, and nodes are removed from the start of the queue. The pseudocode of the BFS algorithm is the following.
procedure BFS_Algorithm(graph, initial_vertex):
create a queue called frontier
create a list called visited_vertex
add the initial vertex in the frontier
while True:
if frontier is empty then
print("No Solution Found")
break
selected_node = remove the first node of the frontier
add the selected_node to the visited_vertex list
// Check if the selected_node is the solution
if selected_node is the solution then
print(selected_node)
break
// Extend the node
new_nodes = extend the selected_node
// Add the extended nodes in the frontier
for all nodes from new_nodes do
if node not in visited_vertex and node not in frontier then
add node at the end of the queue
From the above, it's obvious that in order to solve a problem using a search algorithm like BFS, we must first model the problem in a graph form and then define the initial state of the problem (initial node). After that, we must find the rules that will be followed in order to extend nodes (instances of the problem). These rules are determined by the problem itself. The last thing we need to do is to define the target node or a mechanism so that the algorithm is able to recognize the target node.
Also Read: The theory behind the queue data structure and how the data are stored in a queue
Now that we know how Breadth-First Search (BFS) works, it's time to talk about the problem that we will solve using this algorithm. Suppose there is a maze such as the image shown below and we want to navigate from the entrance to the exit with the less possible movements. As a movement, we consider each movement from one room to another. In our example, the maze consists of eleven rooms each of them has a unique name like “A”, “B”, etc. So, our goal is to navigate from room “S” to “I”.

The initial maze
After defining the problem, it's time to model it into a graph. A very common way to do this is to create a vertex for each room and an edge for each door of the maze. After this modeling, the graph consists of 11 vertices and 15 edges as it seems below.
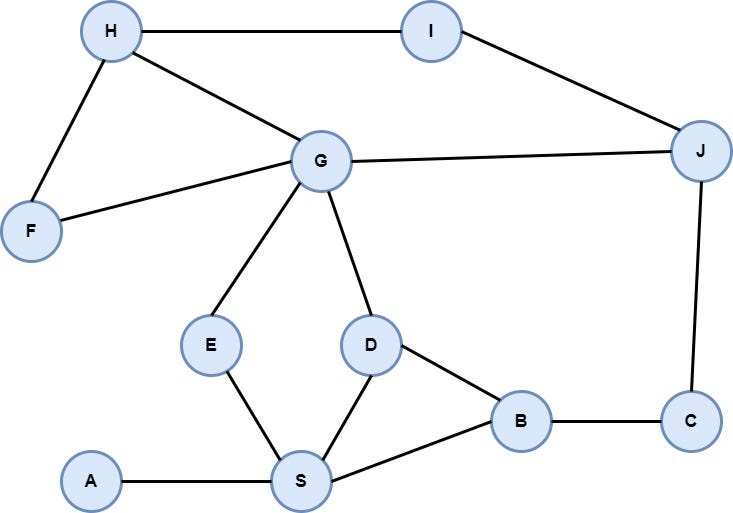
The Graph that represents the above maze
So, from each vertex we can navigate to its neighbors, starting from vertex “S” which is the initial state until the vertex “I” which is the target node of the problem. As I mentioned earlier in this article, the BFS algorithm will explore all nodes at the present level prior to moving on to the nodes at the next level, as it seems in the following image.
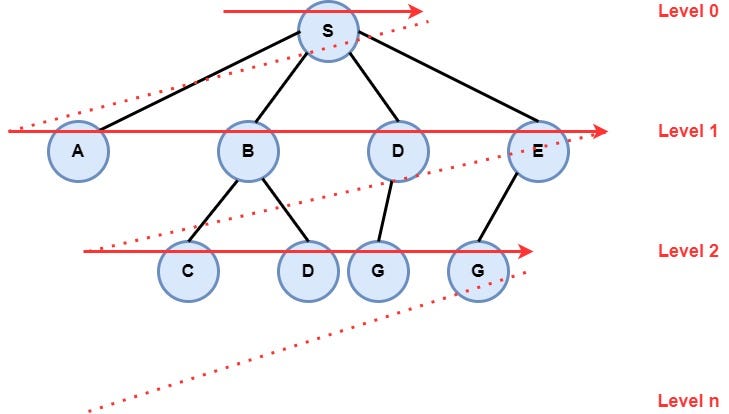
The way that Breadth-First Search Algorithm searches for a solution in the search space
Now that we define and model the problem, we are ready to proceed to the implementation of the algorithm. First, we must represent the maze in our program. Usually, we use an adjacent list or an adjacent table to represent a graph. In our example, we will use a dictionary, so the keys of the dictionary will be the name of the vertices and the value of each key will be a list with all the adjacent vertices of this particular vertex as it seems below.
graph = {
"A": ['S'],
"B": ['C', 'D','S'],
"C": ['B', 'J'],
"D": ['B', 'G', 'S'],
"E": ['G', 'S'],
"F": ['G', 'H'],
"G": ['D', 'E', 'F', 'H', 'J'],
"H": ['F', 'G', 'I'],
"I": ['H', 'J'],
"J": ['C', 'G', 'I'],
"S": ['A', 'B', 'D', 'E']
}
After that, it's time to create the class Node. This class will be implemented as an interface in order to use the same structure of the algorithm for other problems in the future. So, we define abstract methods that users must implement properly according to each problem.
from abc import ABC, abstractmethod
class Node(ABC):
"""
This class used to represent a Node in the graph
It's important to implement this interface in order to make the class BFS more general
and to use it for various problems
...
Methods
-------
__eq__(self, other)
Determines if two nodes are equal or not
is_the_solution(self)
Determines if the current node is the solution of the problem
def is_the_solution(self)
Extends the current node according to the rules of the problem
__str__(self)
Prints the node data
"""
@abstractmethod
def __eq__(self, other):
pass
@abstractmethod
def is_the_solution(self, state):
pass
@abstractmethod
def extend_node(self):
pass
@abstractmethod
def __str__(self):
pass
The next step is to implement the class that represents the Breadth-First Search algorithm. This class contains all necessary methods in order to add a new node to the frontier, to remove a node from the frontier, to check if the frontier is empty and finally to search for a solution in the search space, etc.
class BFS:
"""
This class used to represent the Breadth First Search algorithm (BFS)
...
Attributes
----------
start_state : Node
represent the initial state of the problem
final_state : Node
represent the final state (target) of the problem
frontier : List
represents the stack and is initialized with the start node
checked_nodes : List
represents the list of nodes that have been visited throughout the algorithm execution
number_of_steps : Integer
Keep track of the algorithm's number of steps
path : List
represents the steps from the initial state to the final state
Methods
-------
insert_to_frontier(self, node)
Insert a new node to the frontier. In this algorithm the frontier is a queue, so each new element is inserted to end of the data structure
remove_from_frontier(self)
Remove the first element from the frontier, following the FIFO technic. The removed node is added to the checked_node list
remove_from_frontier(self)
check if the frontier is empty
search(self)
Implements the core of algorithm. This method searches, in the search space of the problem, a solution
"""
def __init__(self, start, final):
self.start_state = start
self.final_state = final
self.frontier = [self.start_state]
self.checked_nodes = []
self.number_of_steps = 0
self.path = []
def insert_to_frontier(self, node):
"""
Insert a node at the end of the frontier
Parameters
----------
node : Node
The node of the problem that will be added to the frontier
"""
self.frontier.append(node)
def remove_from_frontier(self):
"""
Remove a node from the beginning of the frontier
Then add the removed node to the checked_nodes list
Returns
-------
Node
the first node of the frontier
"""
first_node = self.frontier.pop(0)
self.checked_nodes.append(first_node)
return first_node
def frontier_is_empty(self):
"""
Check if the frontier id empty, so no solution found
Returns
-------
Boolean
True if the frontier is empty
False if the frontier is not empty
"""
if len(self.frontier) == 0:
return True
return False
def search(self):
"""
Is the main algorithm. Search for a solution in the solution space of the problem
Stops if the frontier is empty, so no solution found or if find a solution.
"""
while True:
self.number_of_steps += 1
# print(f"Step: {self.number_of_steps}, Frontier Size: {len(self.frontier)} ")
if self.frontier_is_empty():
print(f"No Solution Found after {self.number_of_steps} steps!!!")
break
selected_node = self.remove_from_frontier()
# check if the selected_node is the solution
if selected_node.is_the_solution(self.final_state):
print(f"Solution Found in {self.number_of_steps} steps")
print(selected_node)
break
# extend the node
new_nodes = selected_node.extend_node()
# add the extended nodes in the frontier
if len(new_nodes) > 0:
for new_node in new_nodes:
if new_node not in self.frontier and new_node not in self.checked_nodes:
self.insert_to_frontier(new_node)
After that, we create the class that represents each node of the maze. This class implements the interface Node, implementing all the necessary methods.
from BFS_Algorithm import Node
class MazeNode(Node):
"""
This class used to represent the node of a maze
...
Attributes
----------
graph : Dictionary
represent the graph
value : String
represents the id of the vertex
parent : MazeNode
represents the parent of the current node
Methods
-------
__eq__(self, other)
Determines if the current node is the same with the other
is_the_solution(self, final_state)
Checks if the current node is the solution
extend_node(self)
Extends the current node, creating a new instance of MazeNode for each edge starts from current node
_find_path(self)
Find the path (all verticies and edges from the intitial state to the final state)
__str__(self)
Returns the solution of the maze, the whole path vertex by vertex in order to be printed properly.
"""
def __init__(self, graph, value):
self.graph = graph
self.value = value
self.parent = None
def __eq__(self, other):
"""
Check if the current node is equal with the other node.
Parameters
----------
Other : MazeNode
The other vertex of the graph
Returns
-------
Boolean
True: if both verticies are the same
False: If verticies are different
"""
if isinstance(other, MazeNode):
return self.value == other.value
return self.value == other
def is_the_solution(self, final_state):
"""
Checks if the current node is the solution
Parameters
----------
final_state : MazeNode
The target vertex (final state) of the graph
Returns
-------
Boolean
True: if both verticies are the same, so solution has been found
False: If verticies are different, so solution has not been found
"""
return self.value == final_state
def extend_node(self):
"""
Extends the current node, creating a new instance of MazeNode for each edge starts from the current node
Returns
-------
List
List with all valid new nodes
"""
children = [MazeNode(self.graph, child) for child in self.graph[self.value]]
for child in children:
child.parent = self
return children
def _find_path(self):
"""
Find the path, all verticies and edges from the intitial state to the final state
Returns
-------
List
List with all nodes fron start to end in a row
"""
path = []
current_node = self
while current_node.parent is not None:
path.insert(0, current_node.value)
current_node = current_node.parent
path.insert(0, current_node.value)
return path
def __str__(self):
"""
Returns the solution of the maze, the whole path vertex by vertex as well as the path lenght, in order to be printed properly.
Returns
-------
str
the solution of the problem
"""
total_path = self._find_path()
path = ""
for index in range(len(total_path)):
if index == len(total_path) - 1:
path += f"{total_path[index]} "
else:
path += f"{total_path[index]} -> "
return path + f"\nPath lenght: {len(total_path)-1}"
The last step is to create all the necessary objects and execute the program. After that, the algorithm will compute and print the shortest path from the entrance to the exit of the maze which has a length of 4 and it's the following “S” -> “B” -> “C” -> “J” -> “I”.
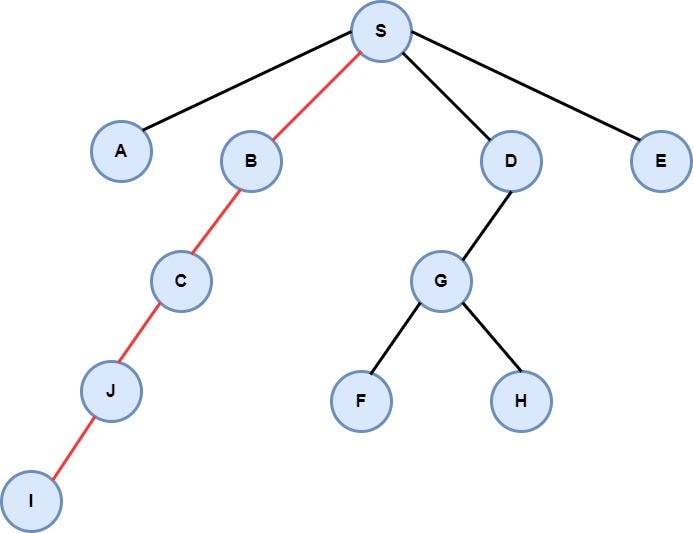
The path from node S to node I
Conclusion
In this article, we talked about Breadth-First Search (BFS) algorithm. We took a look at who this algorithm searches in the search space in order to find a solution to our problem. BFS always returns the solution that is closest to the root, which means that if the cost of each edge is the same for all edges, BFS returns the best solution.
In the second part of the article, we solved the maze problem using the BFS algorithm. Both BFS and DFS algorithms are “blind” algorithms. However, they can be used for lots of problems. In the future, we will have the opportunity to discuss and implement more “clever” algorithms such as the A* algorithm. Until then keep learning and keep coding. Thanks for reading.
P.S You can see the whole source code of the project in this link.
Comments
Loading comments…