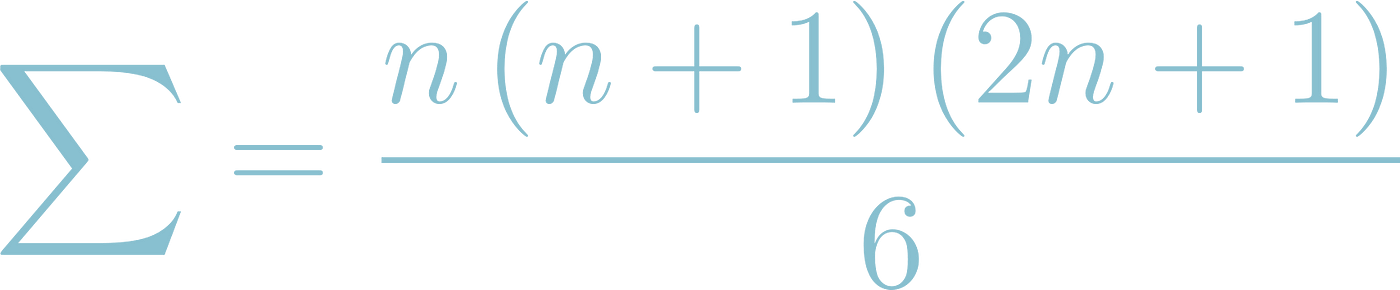Mathematics is arguably the core foundation of computer science. Without its theoretical understanding, computer algorithm is a lifeless bare bone. I have always been fascinated with logical intersection between the two, finding patterns to apply them is just mind-blowing.
Problem Statement
Given a N * N, find the total number of squares that can be extracted from it as illustrated below?
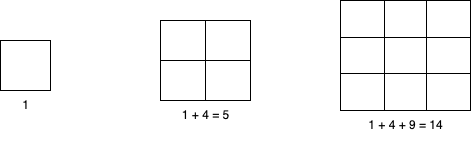
*Explanation: The values in the calculations below are derived from adding the number of combinations that can be formed from groups of smaller squares to form a bigger square, as shown in the table below;*
 Intuition
Intuition
Observing the formation of the number of squares from small values, it can inform derivations that will lead to a more general formula to calculate the number of squares when given N.

*Explanation: A rule of thumb when solving series-based problems is to follow the trail to find a common pattern. In this case, the pattern is consecutive perfect squares.*
Good news — there is a mathematical formula to calculate the summation of consecutive perfect squares;
Programmatically
With the mathematical formula to solve this problem, a basic function can be constructed to compute the total number of squares given N as shown in the python code below;
def get_number_of_squares(n: int) -> int:
return (n * (n + 1) * (2 * n + 1)) // 6
Let’s assume that we do not have a very strong mathematical background to be aware of the existence of such formula, how would we solve such a problem programmatically 🤔?
Well, our intuition unravelled the pattern to be a summation of perfect squares upto the Nth number. With this in mind, the solution approach can thought to be iterative — should be obvious 🧐.
def get_number_of_squares(n):
return sum([i ** 2 for i in range(1, n + 1)])
*Explanation: From 1 to n(well, not quite —second value in range construct is exclusive hence we need to 1 to include n to the computation), get square and sum all the values.*
Dynamic Programming(DP)
We already found multiple ways to find the solution, why do we need Dynamic Programming😩? When mathematics and computer programming intersect, you simply can’t say no to the magic.
Let’s define it; Dynamic programming is defined as a computer programming technique where an algorithmic problem is first broken down into sub-problems, the results are saved, and then the sub-problems are optimized to find the overall solution(spiceworks.com)
In the problem at hand, we clearly found that we can absolutely determine the number of squares given the atomic square unit(where N=1). In other words, we can break the problem into the small possible unit then build up the solution to find the value for N.

*Explanation: Ideally, f(N) should only care about itself and trust that f(N-1) has got every combination upto it. Every time, N wants do computation it will ask N-1 to supplement it with all previous values, N-1 will delay the response since it doesn’t know the value up to itself, it will ask N-2, N-2 doesn’t know the value upto itself either, it will ask N-3 until they reach the atomic unit which is 1. The response will be bubble up until it reaches N as illustrated in the diagram below;*
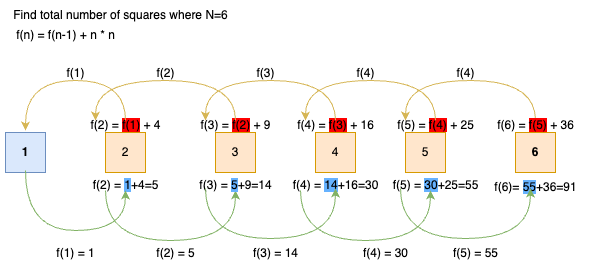
The illustration above is a classic example of recursion, where to compute for N, you have to compute for a variations of N. We know for sure that the base case is 1 which has the total number of squares as 1.
Therefore, we can generalize the computation into a python program shown below;
def get_number_of_squares(n):
if n == 1:
return 1
return get_number_of_squares(n - 1) + n ** 2
*Explanation: When n is 1, we are certain that the total number of squares is 1, but for the rest we have to go top down until the base case(1), then bubble up till we arrive at n with the value it requires to compute it’s total* 👏🏾.
Conclusion
Mathematics is amazing, when you spice it up with programming, you will be amazed the beauty of logical reasoning.
makofi — applause!!