Square roots are useful in a variety of calculations. One simple, yet essential use they have is in the Pythagorean Theorem, which is applied in calculating distances, vector positions and rotations. Even in higher dimensions, the Theorem is similar, applying the square root.
It is a hard operation we tend to underestimate. But in this article, we will dive through the possible algorithms that people have discovered throughout humankind and the math motivation that they have behind them.
Goal: Obtain the square root and the nth root of any real positive number through algorithms using the five basic operations: sum, subtraction, multiplication, division and exponentiation to a natural number.
While there are algorithms that can be extrapolated to the other roots, there might be hard to achieve and go beyond the simplicity this article tries to show. That is why in some algorithms we will only calculate the square root.
To test our algorithms, we will find sqrt(531610), which truncated to the first 10 decimals is 729.1159029948. Also, the number of iterations of all algorithms will be the same: 10 iterations.
1. Approximation Digit by Digit (Any Root)
This is the most straightforward method. It can be interpreted as the brute-force method for obtaining the roots. In other words, it is to get closer and closer, digit by digit. The steps are the following for the square root:
- Find the integer part of the root. To do that, run from 1 to n until n² is bigger than the number. Then, the integer part is n-1.
- Find the first decimal. Iterate through .1 until .9, adding those quantities to the integer part until the number squared is bigger. Then, the result with one decimal is 1/10 less than the number.
- Repeat step 2 with the decimals you want to achieve. You can also do this with any root.
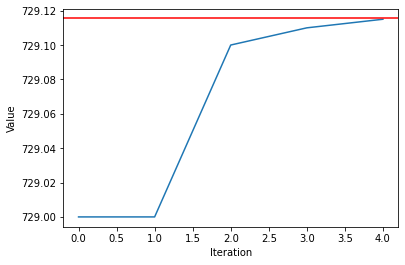
Digit by Digit Method
This is the only method in which we can control the number of decimals of the output, and be sure that they are all correct. However, it is computationally expensive since we need to do a lot of multiplications.
def approx(num, root, n_dec = 10):
nat_num = 1
while nat_num**root <= num:
result = nat_num
nat_num += 1
for d in range(1, n_dec+1):
increment = 10**-d
count = 1
before = result
while (before + increment*count)**root <= num:
result = before + increment*count
count += 1
return round(result, n_dec)
print(approx(531610, 2))
Real Result: 729.1159029948
Output: 729.1159029948. These are the same since we had in the function to get the first 10 decimals. There is no way of quantifying the iterations of this algorithm.
2. Approximation with Binary Search (Any Root)
The motivation is the same as the previous method, but this time we are making use of the binary search.
- Start with an initial guess. For this algorithm, we will choose half of the number.
- Adjust the value. If the guess squared is smaller, make bigger the value in a step of 1/2^index. If the guess squared is bigger, make smaller the value in the same quantity.
- Repeat step 2, until you have the desired precision.
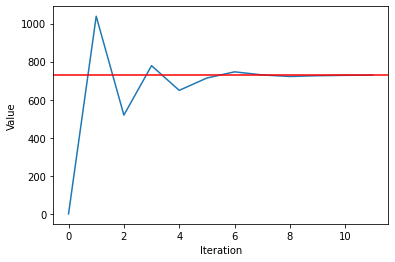
Binary Search
This method is faster than the previous one because it needs to perform fewer operations; it is a linear search against binary search.
def binary(num, root):
guess = num/2
for term in range(1, 1):
exp = guess ** root
if exp > num:
guess = guess - (num/(2**term))
elif exp < num:
guess = guess + (num/(2**term))
else:
break
return guess
print(binary(531610, 2))
Real Result: 729.1159029948
Output: 519.15039062. This result is disappointing, but picture the following: we are trying to find the square root by looking through the continuum of real numbers, a hard task to achieve in 10 iterations. However, I promise that if you set the number of iterations to 40, you will achieve up to 5 correct decimal places!
Luckily we have more interesting algorithms using series and math tricks to get quicker the result, as you will see on the next one, which is probably the most famous one.
3. Babylonian Method (Square Root)
This is an ancient and elegant method of finding the square root coming from the Babylonians.
- Make an initial guess. Normally it is chosen to 1.
- Apply the recursive formula.
- Repeat until you get close enough to the root.
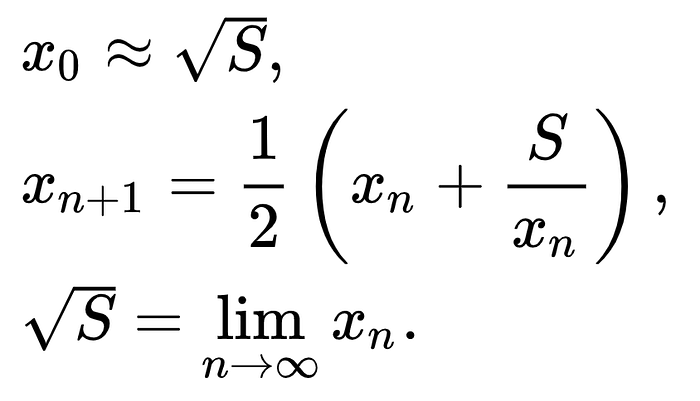
Babylonian Method formulas. Source: Wikipedia
def babylonian(num):
for term in range(10):
if term == 0:
x = 1
x = (x+(num/x))/2
return x
print(babylonian(531610))
Real Result: 729.1159029948
Output: 822.6440066567137
4. Newton’s Method (Any Root)
Surprisingly, the Babylonian Method is Newton’s Method applied for the square root. Nevertheless, we can use Newton’s method for a bunch of other functions — including any root.
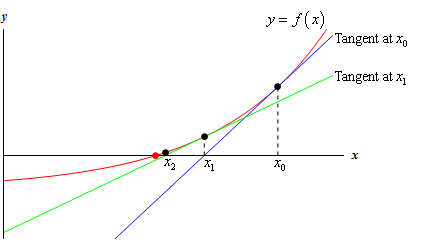
Newton’s Method Visual. Source: Pauls Online Math Notes
The idea of this algorithm is extremely elegant and is one of the many applications of calculus.
- Express a function, where the root is a solution to our equation, specifically f(x) = x²-n = 0.
- Use the recursive formula. In this case, we will apply it 10 times.
- Repeat.

Newton’s Method Formula. Source: BragittOff.com
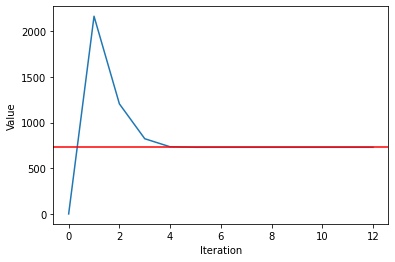
Babylonian and Newton’s method for Square Root
def newton(num, root):
for iter in range(10):
if iter == 0:
x = 1 f = x**root - num
g = root*(x**(root-1))
x = x - (f/g)
return x
print(newton(531610, 2))
5. Taylor Series (Square Root)
This is the trickiest one, but also the most satisfying and complex of the methods shown. It all comes down to this formula:
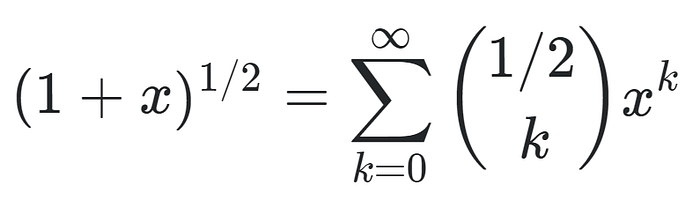
Generalized binomial theorem for square roots. Source: Math Stack exchange
Which use some very interesting properties of the binomial coefficients. One important thing to note is that the formula above only converges if the absolute value of x is less than or equal to 1. That means we cannot put any value of x.
Nevertheless, we can use a simple trick:
- Transform the number into a decimal one. For instance, we divide it into a power of 10 (like in scientific notation) to obtain it into a decimal and then subtract one from it.
- Apply the formula above. In this case, we will sum 10 terms.
- Undo the transformation. This will give us the result.
To achieve this, we will have to create a binomial coefficient function and a factorial one. But don’t scare, they’re pretty simple.
def fact(n):
if n == 1 or n==0:
return 1
else:
return n*fact(n-1)
def bin_coef(m, k): # m choose k
numerator = 1
for factor in range(0, k):
numerator = numerator*(m-factor)
denominator = fact(k)
coef = numerator/denominator
return coef
def taylor(num):
exp = len(str(num))
x = (num/(10**exp))-1
sum = 0
for term in range(10):
sum += bin_coef(1/2, term) * (x**term)
if exp % 2 == 0:
result = sum*(10**(exp/2))
else:
result = sum*3.16227766017*(10**((exp-1)/2))
return result
print(taylor(531610))
Real Result: 729.1159029948
Output: 729.123862916769. Much better!
6. Logarithmic Properties (Any Root)
We can convert our problems into other ones which we know how to do them. In this case, there are quick ways to obtain the exponent function and the natural logarithm. We just add a division in the process… and the square root is obtained!
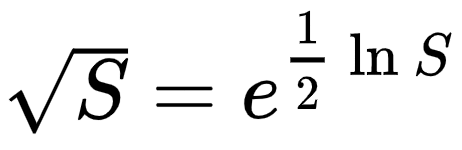
Using Logarithms to our advantage. Source: Wikipedia
- Calculate ln(S) with a quick convergence sum, and divide by 2.
- Raise e to the number, using the Taylor Series for e^x.
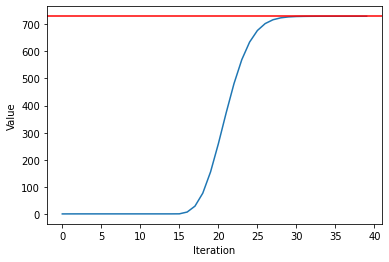
Logarithmic Properties
def logarithms(num, root):
dec = len(str(num))-1
A = num / (10**dec)
y = (A-1)/(A+1)
sum = 0
for term in range(10):
sum += (y**(2*term+1)) / (2*term+1)
sum = sum*2
ln = dec*2.30258509299 + sum
exp = ln / root
sum = 0
for term in range(10):
sum += (exp**term) / fact(term)
return sum
print(logarithms(531610, 2))
Real Result: 729.1159029948
Output: 633.852144487265
Comparison between the Algorithms
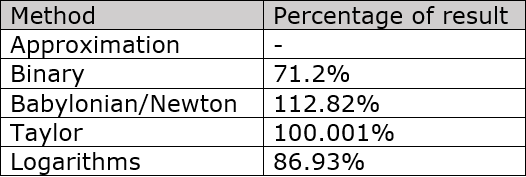
Table of Comparison
In the end, 10 iterations were too low. But still, we got some pretty accurate results!
Extra Two Ways — For the curious
7. By Hand Method
There is a way to get the square root by a process similar to the long division. The article below shows the process and why it is true. I recommend you check it out!
8. Fast Inverse Square Root
For a cool explanation of one of the quickest and most efficient ways to calculate the square roots, you should watch this video to become delighted.
One of the fastest ways to obtain a square root.
Luckily, in Python, we can use the powerful exponent operator to obtain the square root, but at least we now know a bunch of ways to compute it and what’s behind the scenes in this type of operation. I hope you liked the article!
sqrt = 531610 ** (0.5)
Sources
This article would not have been possible with the following math communities and articles:
Methods of computing square roots - Wikipedia
Taylor series of $\sqrt{1+x}$ using sigma notation
Binomial coefficients $1/2\choose k$
Is there an approximation to the natural log function at large values?
Comments
Loading comments…