In this article, I will introduce how to use Hungarian Method to resolve the linear assignment problem and provide my personal Python code solution.
So… What is the linear assignment problem?
The linear assignment problem represents the need to maximize the available resources (or minimize the expenditure) with limited resources. For instance, below is a 2D matrix, where each row represents a different supplier, and each column represents the cost of employing them to produce a particular product. Each supplier can only specialize in the production of one of these products. In other words, only one element can be selected for each column and row in the matrix, and the sum of the selected elements must be minimized (minimized cost expense).
The cost of producing different goods by different producers:
Indeed, this is a simple example. By trying out the possible combinations, we can see that the smallest sum is 13, so supplier A supplies Bubble Tea, supplier B supplies milk tea, and supplier C supplies Fruit Tea. However, such attempts do not follow a clear rule and become inefficient when applied to large tasks. Therefore, the next section will introduce step by step the Hungarian algorithm, which can be applied to the linear assignment problem.
Hungarian Algorithm & Python Code Step by Step
In this section, we will show how to use the Hungarian algorithm to solve linear assignment problems and find the minimum combinations in the matrix. Of course, the Hungarian algorithm can also be used to find the maximum combination.
Step 0. Prepare Operations
First, an N by N matrix is generated to be used for the Hungarian algorithm (Here, we use a 5 by 5 square matrix as an example).
import numpy as np
cost_matrix = np.random.randint(10,size=(5, 5))
print(f"The cost matrix is:\n", cost_matrix)
The above code randomly generates a 5x5 cost matrix of integers between 0 and 10.
If we want to find the maximum sum, we could do the opposite. The matrix to be solved is regarded as the profit matrix, and the maximum value in the matrix is set as the common price of all goods. The cost matrix is obtained by subtracting the profit matrix from the maximum value. Finally, the cost matrix is substituted into the Hungarian algorithm to obtain the minimized combination and then remapped back to the profit matrix to obtain the maximized sum value and composition result.
import numpy as np
#The matrix who you want to find the maximum sum
profit_matrix = np.random.randint(10,size=(5, 5))
#Using the maximum value of the profit_matrix to get the corresponding cost_matrix
max_value = np.max(profit_matrix)
#Using the cost matrix to find which positions are the answer
cost_matrix = max_value - profit_matrix
print(f"The profit matrix is:\n", profit_matrix, f"\nThe cost matrix is:\n", cost_matrix)
The above code randomly generates a 5x5 profit matrix of integers between 0 and 10 and generate a corresponding cost matrix
By following the steps above, you can randomly generate either the cost matrix or the profit matrix. Next, we will move into the introduction of the Hungarian algorithm, and for the sake of illustration, the following sections will be illustrated using the cost matrix shown below. We will use the Hungarian algorithm to solve the linear assignment problem of the cost matrix and find the corresponding minimum sum.
Example cost matrix:
Step 1. Every column and every row subtract its internal minimum
First, every column and every row must subtract its internal minimum. After subtracting the minimum, the cost matrix will look like this.
Cost matrix after step 1:
And the current code is like this:
import numpy as np
def hungarian_algorithm(mat):
dim = mat.shape[0]
cur_mat = mat
#Step 1 - Every column and every row subtract its internal minimum
for row_num in range(mat.shape[0]):
cur_mat[row_num] = cur_mat[row_num] - np.min(cur_mat[row_num])
for col_num in range(mat.shape[1]):
cur_mat[:,col_num] = cur_mat[:,col_num] - np.min(cur_mat[:,col_num])
def main():
#The matrix who you want to find the maximum sum
cost_matrix = np.array([[7, 6, 2, 9, 2],
[6, 2, 1, 3, 9],
[5, 6, 8, 9, 5],
[6, 8, 5, 8, 6],
[9, 5, 6, 4, 7]])
ans_pos = hungarian_algorithm(cost_matrix.copy())
if __name__ == '__main__':
main()
Step 2.1. Min_zero_row Function Implementation
At first, we need to find the row with the fewest zero elements. So, we can convert the previous matrix to the boolean matrix(0 → True, Others → False).
Transform matrix to boolean matrix:
import numpy as np
#Transform the matrix to boolean matrix(0 = True, others = False)
zero_bool_mat = (cur_mat == 0)
Corresponding Boolean matrix:
Therefore, we can use the “min_zero_row” function to find the corresponding row.
# zero_mat = boolean, mark_zero = blank list
def min_zero_row(zero_mat, mark_zero):
'''
The function can be splitted into two steps:
#1 The function is used to find the row which containing the fewest 0.
#2 Select the zero number on the row, and then marked the element corresponding row and column as False
'''
#Find the row
min_row = [99999, -1]
for row_num in range(zero_mat.shape[0]):
if np.sum(zero_mat[row_num] == True) > 0 and min_row[0] > np.sum(zero_mat[row_num] == True):
min_row = [np.sum(zero_mat[row_num] == True), row_num]
The row which contains the least 0:

Third, mark any 0 elements on the corresponding row and clean up its row and column (converts elements on the Boolean matrix to False). The coordinates of the element are stored in mark_zero.
# zero_mat = boolean matrix, mark_zero = blank list
def min_zero_row(zero_mat, mark_zero):
'''
The function can be splitted into two steps:
#1 The function is used to find the row which containing the fewest 0.
#2 Select the zero number on the row, and then marked the element corresponding row and column as False
'''
#Find the row
min_row = [99999, -1]
for row_num in range(zero_mat.shape[0]):
if np.sum(zero_mat[row_num] == True) > 0 and min_row[0] > np.sum(zero_mat[row_num] == True):
min_row = [np.sum(zero_mat[row_num] == True), row_num]
# Marked the specific row and column as False
zero_index = np.where(zero_mat[min_row[1]] == True)[0][0]
mark_zero.append((min_row[1], zero_index))
zero_mat[min_row[1], :] = False
zero_mat[:, zero_index] = False
Hence, the boolean matrix will look like this:
The boolean matrix after the first process. The fourth row has been changed to all False.
The process is repeated several times until the elements in the boolean matrix are all False. The below picture shows the order in which they are marked.
The possible answer composition:

Step 2.2. Mark_matrix Function Implementation
After getting Zero_mat from the step 2–1, we can check it and mark the matrix according to certain rules. The whole rule can be broken down into several steps:
- Mark rows that do not contain marked 0 elements and store row indexes in the non_marked_row
- Search non_marked_row element, and find out if there are any unmarked 0 elements in the corresponding column
- Store the column indexes in the marked_cols
- Compare the column indexes stored in marked_zero and marked_cols
- If a matching column index exists, the corresponding row_index is saved to non_marked_rows
- Next, the row indexes that are not in non_marked_row are stored in marked_rows
Finally, the whole mark_matrx function is finished and then returns marked_zero, marked_rows, marked_cols. At this point, we will be able to decide the result based on the return information.
def mark_matrix(mat):
'''
Finding the returning possible solutions for LAP problem.
'''
#Transform the matrix to boolean matrix(0 = True, others = False)
cur_mat = mat
zero_bool_mat = (cur_mat == 0)
zero_bool_mat_copy = zero_bool_mat.copy()
#Recording possible answer positions by marked_zero
marked_zero = []
while (True in zero_bool_mat_copy):
min_zero_row(zero_bool_mat_copy, marked_zero)
#Recording the row and column indexes seperately.
marked_zero_row = []
marked_zero_col = []
for i in range(len(marked_zero)):
marked_zero_row.append(marked_zero[i][0])
marked_zero_col.append(marked_zero[i][1])
#step 2-2-1
non_marked_row = list(set(range(cur_mat.shape[0])) - set(marked_zero_row))
marked_cols = []
check_switch = True
while check_switch:
check_switch = False
for i in range(len(non_marked_row)):
row_array = zero_bool_mat[non_marked_row[i], :]
for j in range(row_array.shape[0]):
#step 2-2-2
if row_array[j] == True and j not in marked_cols:
#step 2-2-3
marked_cols.append(j)
check_switch = True
for row_num, col_num in marked_zero:
#step 2-2-4
if row_num not in non_marked_row and col_num in marked_cols:
#step 2-2-5
non_marked_row.append(row_num)
check_switch = True
#step 2-2-6
marked_rows = list(set(range(mat.shape[0])) - set(non_marked_row))
return(marked_zero, marked_rows, marked_cols)
If we use the example cost matrix, the corresponding marked_zero, marked_rows, and marked_cols are as follows:
- marked_zero: [(3, 2), (0, 4), (1, 1), (2, 0), (4, 3)]
- marked_rows: [0, 1, 2, 3, 4]
- marked_cols: []
Step 3. Identify the Result
At this step, if the sum of the lengths of marked_rows and marked_cols is equal to the length of the cost matrix, it means that the solution of the linear assignment problem has been found successfully, and marked_zero stores the solution coordinates. Fortunately, in the example matrix, we find the answer on the first try. Therefore, we can skip to step 5 and calculate the solution.
However, everything is hardly plain sailing. Most of the time, we will not find the solution on the first try, such as the following matrix:
After Step 1 & 2, the corresponding matrix, marked_rows, and marked_cols are as follows:
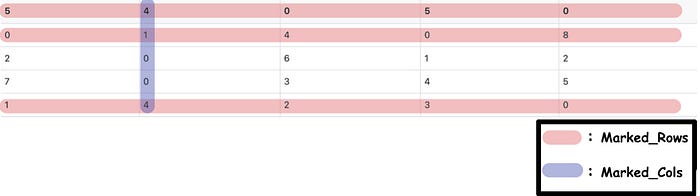
The sum of the lengths of Marked_Rows and Marked_Cols is 4 (less than 5).
Apparently, the sum of the lengths is less than the length of the matrix. At this time, we need to go into Step 4 to adjust the matrix.
def hungarian_algorithm(mat):
dim = mat.shape[0]
cur_mat = mat
#Step 1 - Every column and every row subtract its internal minimum
for row_num in range(mat.shape[0]):
cur_mat[row_num] = cur_mat[row_num] - np.min(cur_mat[row_num])
for col_num in range(mat.shape[1]):
cur_mat[:,col_num] = cur_mat[:,col_num] - np.min(cur_mat[:,col_num])
zero_count = 0
while zero_count < dim:
#Step 2 & 3
ans_pos, marked_rows, marked_cols = mark_matrix(cur_mat)
zero_count = len(marked_rows) + len(marked_cols)
if zero_count < dim:
cur_mat = adjust_matrix(cur_mat, marked_rows, marked_cols)
return ans_pos
Step 4. Adjust Matrix
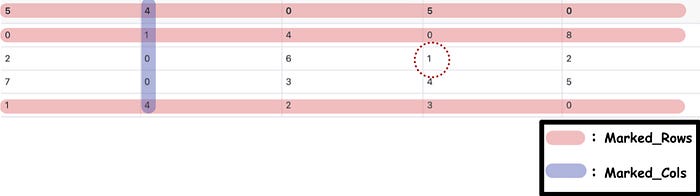
In Step 4, we're going to put the matrix after Step 1 into the Adjust_Matrix function. Taking the latter matrix in Step 3 as an example, the matrix to be modified in Adjust_Matrix is:
The whole function can be separated into three steps:
- Find the minimum value for an element that is not in marked_rows and not in marked_cols. Hence, we can find the minimum value is 1.
def adjust_matrix(mat, cover_rows, cover_cols):
cur_mat = mat
non_zero_element = []
#Step 4-1 Find the minimum value
for row in range(len(cur_mat)):
if row not in cover_rows:
for i in range(len(cur_mat[row])):
if i not in cover_cols:
non_zero_element.append(cur_mat[row][i])
min_num = min(non_zero_element)
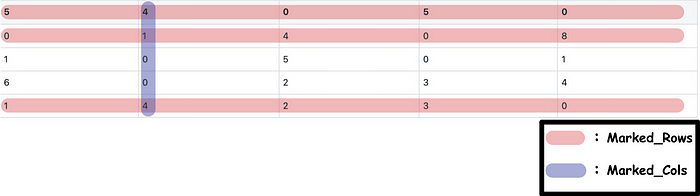
- Subtract the elements which not in marked_rows nor marked_cols from the minimum values obtained in the previous step.
def adjust_matrix(mat, cover_rows, cover_cols):
cur_mat = mat
non_zero_element = []
#Step 4-1
for row in range(len(cur_mat)):
if row not in cover_rows:
for i in range(len(cur_mat[row])):
if i not in cover_cols:
non_zero_element.append(cur_mat[row][i])
min_num = min(non_zero_element)
#Step4-2
for row in range(len(cur_mat)):
if row not in cover_rows:
for i in range(len(cur_mat[row])):
if i not in cover_cols:
cur_mat[row, i] = cur_mat[row, i] - min_num
- Add the element in marked_rows, which is also in marked_cols, to the minimum value obtained by Step 4–1.

def adjust_matrix(mat, cover_rows, cover_cols):
cur_mat = mat
non_zero_element = []
#Step 4-1
for row in range(len(cur_mat)):
if row not in cover_rows:
for i in range(len(cur_mat[row])):
if i not in cover_cols:
non_zero_element.append(cur_mat[row][i])
min_num = min(non_zero_element)
#Step 4-2
for row in range(len(cur_mat)):
if row not in cover_rows:
for i in range(len(cur_mat[row])):
if i not in cover_cols:
cur_mat[row, i] = cur_mat[row, i] - min_num
#Step 4-3
for row in range(len(cover_rows)):
for col in range(len(cover_cols)):
cur_mat[cover_rows[row], cover_cols[col]] = cur_mat[cover_rows[row], cover_cols[col]] + min_num
return cur_mat
Return the adjusted matrix and repeat Step 2 and Step 3 until the conditions satisfy the requirement of entering Step 5.
Step 5. Calculate the Answer
Using the element composition stored in marked_zero, the minimum and maximum values of the linear assignment problem can be calculated.

The minimum composition of the assigned matrix and the minimum sum is 18.

The maximum composition of the assigned matrix and the maximum sum is 43.
The code of the Answer_Calculator function is as follows:
def ans_calculation(mat, pos):
total = 0
ans_mat = np.zeros((mat.shape[0], mat.shape[1]))
for i in range(len(pos)):
total += mat[pos[i][0], pos[i][1]]
ans_mat[pos[i][0], pos[i][1]] = mat[pos[i][0], pos[i][1]]
return total, ans_mat
Conclusion
The complete code is as follows:
import numpy as np
def min_zero_row(zero_mat, mark_zero):
'''
The function can be splitted into two steps:
#1 The function is used to find the row which containing the fewest 0.
#2 Select the zero number on the row, and then marked the element corresponding row and column as False
'''
#Find the row
min_row = [99999, -1]
for row_num in range(zero_mat.shape[0]):
if np.sum(zero_mat[row_num] == True) > 0 and min_row[0] > np.sum(zero_mat[row_num] == True):
min_row = [np.sum(zero_mat[row_num] == True), row_num]
# Marked the specific row and column as False
zero_index = np.where(zero_mat[min_row[1]] == True)[0][0]
mark_zero.append((min_row[1], zero_index))
zero_mat[min_row[1], :] = False
zero_mat[:, zero_index] = False
def mark_matrix(mat):
'''
Finding the returning possible solutions for LAP problem.
'''
#Transform the matrix to boolean matrix(0 = True, others = False)
cur_mat = mat
zero_bool_mat = (cur_mat == 0)
zero_bool_mat_copy = zero_bool_mat.copy()
#Recording possible answer positions by marked_zero
marked_zero = []
while (True in zero_bool_mat_copy):
min_zero_row(zero_bool_mat_copy, marked_zero)
#Recording the row and column positions seperately.
marked_zero_row = []
marked_zero_col = []
for i in range(len(marked_zero)):
marked_zero_row.append(marked_zero[i][0])
marked_zero_col.append(marked_zero[i][1])
#Step 2-2-1
non_marked_row = list(set(range(cur_mat.shape[0])) - set(marked_zero_row))
marked_cols = []
check_switch = True
while check_switch:
check_switch = False
for i in range(len(non_marked_row)):
row_array = zero_bool_mat[non_marked_row[i], :]
for j in range(row_array.shape[0]):
#Step 2-2-2
if row_array[j] == True and j not in marked_cols:
#Step 2-2-3
marked_cols.append(j)
check_switch = True
for row_num, col_num in marked_zero:
#Step 2-2-4
if row_num not in non_marked_row and col_num in marked_cols:
#Step 2-2-5
non_marked_row.append(row_num)
check_switch = True
#Step 2-2-6
marked_rows = list(set(range(mat.shape[0])) - set(non_marked_row))
return(marked_zero, marked_rows, marked_cols)
def adjust_matrix(mat, cover_rows, cover_cols):
cur_mat = mat
non_zero_element = []
#Step 4-1
for row in range(len(cur_mat)):
if row not in cover_rows:
for i in range(len(cur_mat[row])):
if i not in cover_cols:
non_zero_element.append(cur_mat[row][i])
min_num = min(non_zero_element)
#Step 4-2
for row in range(len(cur_mat)):
if row not in cover_rows:
for i in range(len(cur_mat[row])):
if i not in cover_cols:
cur_mat[row, i] = cur_mat[row, i] - min_num
#Step 4-3
for row in range(len(cover_rows)):
for col in range(len(cover_cols)):
cur_mat[cover_rows[row], cover_cols[col]] = cur_mat[cover_rows[row], cover_cols[col]] + min_num
return cur_mat
def hungarian_algorithm(mat):
dim = mat.shape[0]
cur_mat = mat
#Step 1 - Every column and every row subtract its internal minimum
for row_num in range(mat.shape[0]):
cur_mat[row_num] = cur_mat[row_num] - np.min(cur_mat[row_num])
for col_num in range(mat.shape[1]):
cur_mat[:,col_num] = cur_mat[:,col_num] - np.min(cur_mat[:,col_num])
zero_count = 0
while zero_count < dim:
#Step 2 & 3
ans_pos, marked_rows, marked_cols = mark_matrix(cur_mat)
zero_count = len(marked_rows) + len(marked_cols)
if zero_count < dim:
cur_mat = adjust_matrix(cur_mat, marked_rows, marked_cols)
return ans_pos
def ans_calculation(mat, pos):
total = 0
ans_mat = np.zeros((mat.shape[0], mat.shape[1]))
for i in range(len(pos)):
total += mat[pos[i][0], pos[i][1]]
ans_mat[pos[i][0], pos[i][1]] = mat[pos[i][0], pos[i][1]]
return total, ans_mat
def main():
'''Hungarian Algorithm:
Finding the minimum value in linear assignment problem.
Therefore, we can find the minimum value set in net matrix
by using Hungarian Algorithm. In other words, the maximum value
and elements set in cost matrix are available.'''
#The matrix who you want to find the minimum sum
cost_matrix = np.array([[7, 6, 2, 9, 2],
[6, 2, 1, 3, 9],
[5, 6, 8, 9, 5],
[6, 8, 5, 8, 6],
[9, 5, 6, 4, 7]])
ans_pos = hungarian_algorithm(cost_matrix.copy())#Get the element position.
ans, ans_mat = ans_calculation(cost_matrix, ans_pos)#Get the minimum or maximum value and corresponding matrix.
#Show the result
print(f"Linear Assignment problem result: {ans:.0f}\n{ans_mat}")
#If you want to find the maximum value, using the code as follows:
#Using maximum value in the cost_matrix and cost_matrix to get net_matrix
profit_matrix = np.array([[7, 6, 2, 9, 2],
[6, 2, 1, 3, 9],
[5, 6, 8, 9, 5],
[6, 8, 5, 8, 6],
[9, 5, 6, 4, 7]])
max_value = np.max(profit_matrix)
cost_matrix = max_value - profit_matrix
ans_pos = hungarian_algorithm(cost_matrix.copy())#Get the element position.
ans, ans_mat = ans_calculation(profit_matrix, ans_pos)#Get the minimum or maximum value and corresponding matrix.
#Show the result
print(f"Linear Assignment problem result: {ans:.0f}\n{ans_mat}")
if __name__ == '__main__':
main()
References
Comments
Loading comments…