
The sine took time to make. Python Icon made by [Freepik](https://www.freepik.com/) from [Flaticon](https://www.flaticon.com/).
Two years ago when I was a wee young lad with coding chops kinda restricted to loops and conditionals, I wanted to make a synth, because synths are awesome. But I couldn't. 😐
Recently, when I was freestyling on Jupyter, as one does given a dearth of friends, and an affinity for code, I realised synths aren't that difficult to code out, they are just generators of periodic sequences of numbers that are fed really quickly into a speaker.
So I gave it a shot, and I was right. Anyways, this series of posts is about how you synthesize sounds using Python.
4 oscillators playing A4, A3, A2, A1
Preliminaries 🔈
This is a skippable section that glosses over digital sound, lazy iteration and synths before the main thing: oscillators.
Digital Sound 💿
First, a note on digital sound because that's what's gonna be generated. Digital sound is just a sequence of numbers being fed to a speaker from a computer at a certain speed, I'm oversimplifying but that's basically what happens.
If one is talking about CD Audio (which no one talks about now days), 44,100 numbers each having a value between -32,768 and 32,767 are being fed to the speaker through some circuitry (a DAC) every second which means that CD Audio has a sample rate of 44,100Hz and a bit depth of 16 bits (signed integers).
So to generate sound all we need to do is create a stream of sensible integers and point the stream to a speaker or a file. The nuances of this pointing can be handled by libraries.
Lazy Iteration 💤
Lazy iteration is like normal iteration, but a value is evaluated only when we need it, for example we need a note to be played only when we press a key, so the values of the note can be evaluated when we press the key rather than before it.
For lazy iteration of a sequence we can use two different Python features
- Generators
- Iterators
All generators are iterators, and an object is an iterator only if it implements the __next__ and the __iter__ functions in it's class definition. A generator can be implemented using a generator expression, such as:
processed_values_gen = (some_function(i) for i in range(30))
which looks like list comprehension but with regular brackets, or a generator function, such as:
def generator_function():
for i in range(30):
yield some_function(i)
which is a function that has a yield instead of a return which is what makes it a generator. Once you have a generator or an iterator a value can be obtained from it by calling the next function on it like so:
processed_values_gen = generator_function()
next(processed_values_gen)
I won't be covering the intricacies of the two cause the article may end up being too long, this Stack Overflow post explains the difference between the two; here's a link that explains generators, and another that explains iterators quite well.
Using generators and iterators we can generate infinite streams of integers which can be fed to some output like a speaker or a file, without these features the memory requirements would be very high.
Synthesizers 🎛
To avoid confusion :
A synthesizer is an electric instrument. A keyboard is a form of input. A piano is a keyboarded acoustic instrument.

An old school synth, a [Moog Modular System 55](https://www.moogmusic.com/news/return-moog-modular).
A synthesizer is something that makes (synthesizes) it's own sound from scratch. A synthesizer is an electric instrument it can be analog (like the Moog Modular) or digital (like the NI Massive).
A synthesizer can have different kinds of controllers such as pressure sensitive pads or keyboards 🎹 which send control signals to the synthesizer, which then synthesizes the sound, the sound is then sent to a speaker for playback.
Synths can be really complex, I mean just look at the Moog Modular above, one would probably need an Electrical Engineering degree to operate it.
To overly simplify a synth, it consists of components that generate the sound such as oscillators, and components that shape the sound such as envelopes and LFOs (Low Frequency Oscillators), and maybe even components that add effects to the sounds such as a vibrato, or a tremolo. A few of these components I'll try and cover in these posts.
Oscillators, The Beginning 🌅
An oscillator is probably the most important component of a synthesizer 🫀, it is a component that generates a sequence of numbers that repeat after a certain interval. The most simplest oscillator is one that produces a sine wave which is generated by, unsurprisingly yet delightfully, the sine function.
A Simple Sine 👶
The sine wave repeats with a time period of 2π, so if we have to generate a 1 Hz signal with a sample rate of 512 Hz we'd have to create 512 divisions on a number line between 0 and 2π and at each division we apply the mathematical sine function which gives us an output sample of the sine wave at that division.
This sine wave when played at 512 samples per second will give us a 1 Hz signal which (in 2021) we won't be able to hear cause that's infrasonic.
Since we don't want to generate all the samples at once, we can just increment the input to the sin by a step size when the next sample is required, the step size can be calculated by this:
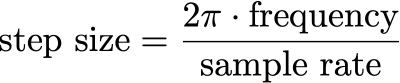
Using the math and the itertools library we can now create a sine wave generator using the above formula.
The above function returns a generator so to evaluate the first 512 samples of the generator we can use the following code
osc = get_sin_oscillator(freq=1, sample_rate=512)
samples = [next(osc) for i in range(512)]
In the above snippet I'm using Python list comprehension to get the first 512 samples of a 1 Hz sine wave that has been sampled at 512 Hz.
And this is how it looks:
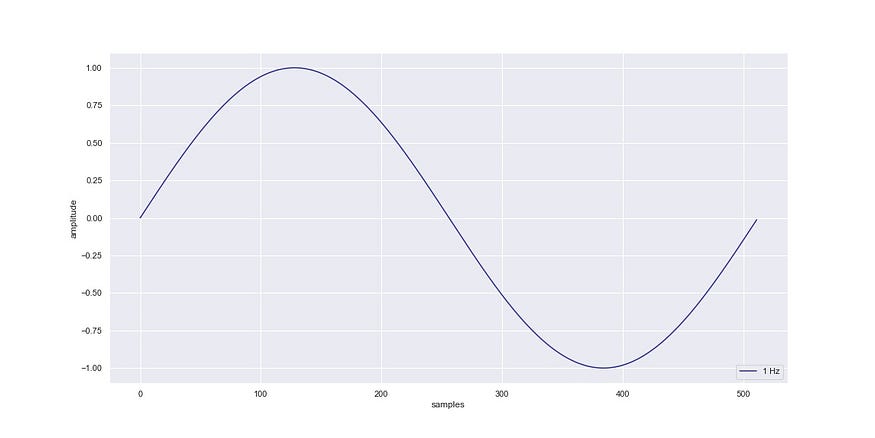
A 1 Hz sine wave sampled at 512 Hz.
Note : For all other plots and wave generations I'll be using a sample rate of 44,100 Hz.
Oscillator Parameters 🎚
In an oscillator there are a few parameters that can be controlled, the most obvious one is the frequency of an oscillator, altering this gives us different notes. For example: middle C or C4 has a frequency of 261.625565 Hz when tuned to concert pitch, i.e. when A4 has a frequency of 440 Hz.
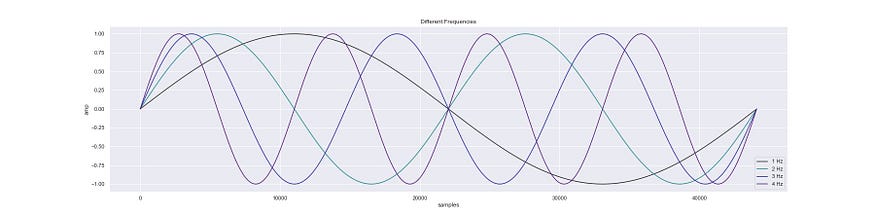
Sine waves at 4 different frequencies.
Other than frequency, we can control amplitude which can give us effects such as vibrato, or just plain old volume control. We can control this by just multiplying the output value of an oscillator with a number between 0 and 1.
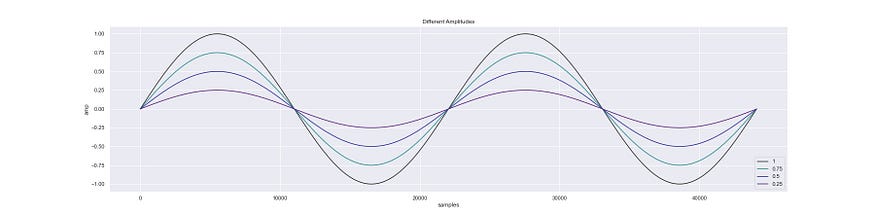
Sine waves at 4 different amplitudes.
Another less obvious one is phase which can give us effects such as a phaser. This can be achieved by adding the phase angle, which has a value between 0 and 360, to the sine function input.
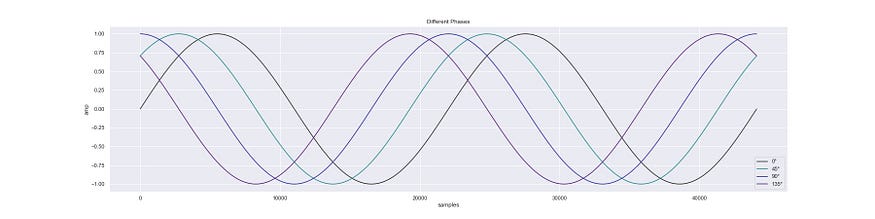
Sine waves at 4 different phase angles.
All of the three plots above were obtained by using this function:
def get_sin_oscillator(freq, amp=1, phase=0, sample_rate=44100):
phase = (phase / 360) * 2 * math.pi
increment = (2 * math.pi * freq)/ sample_rate
return (math.sin(phase + v) * amp for v in itertools.count(start=0, step=increment))
which is nice cause our oscillator fits in 4 lines, but it would be much nicer if we could adjust these three parameters on the fly i.e. without having to create a new generator everytime an adjustment is made, this would allow us to hook oscillators up with other oscillators to obtain all kinds of fun sounds, this covers a lot of what happens in synthesizers, oscillators oscillating oscillators; wub-wub.
Note : If you want to skip to making a simple sine oscillator synth then check the third post.
Oscillators, A Journey Into OOP
Now I realize that OOP maybe your least favourite programming paradigm, one that conjures up memories of Java induced trauma, but at some point when writing this, I found OOP to be kinda apt for oscillator design.
The ABC 🏛
The point of this section is to build an oscillator that allows us to change the three parameters on the fly. So here I'll first define an abstract base class that we'll flesh out to build our oscillator.
from abc import ABC, abstractmethod
class Oscillator(ABC):
def __init__(self, freq=440, phase=0, amp=1, \
sample_rate=44_100, wave_range=(-1, 1)):
self._freq = freq
self._amp = amp
self._phase = phase
self._sample_rate = sample_rate
self._wave_range = wave_range
### Properties that will be changed
self._f = freq
self._a = amp
self._p = phase
@property
def init_freq(self):
return self._freq
@property
def init_amp(self):
return self._amp
@property
def init_phase(self):
return self._phase
@property
def freq(self):
return self._f
@freq.setter
def freq(self, value):
self._f = value
self._post_freq_set()
@property
def amp(self):
return self._a
@amp.setter
def amp(self, value):
self._a = value
self._post_amp_set()
@property
def phase(self):
return self._p
@phase.setter
def phase(self, value):
self._p = value
self._post_phase_set()
def _post_freq_set(self):
pass
def _post_amp_set(self):
pass
def _post_phase_set(self):
pass
@abstractmethod
def _initialize_osc(self):
pass
@staticmethod
def squish_val(val, min_val=0, max_val=1):
return (((val + 1) / 2 ) * (max_val - min_val)) + min_val
@abstractmethod
def __next__(self):
return None
def __iter__(self):
self.freq = self._freq
self.phase = self._phase
self.amp = self._amp
self._initialize_osc()
I know, I know, I realize that you came here probably wanting to learn about synths, and now maybe flustered seeing the eighty something lines of OOP code I have thrown at you, but just bear with me it gets interesting after the OOP hurdle is crossed.
The above Abstract Base Class basically lays out the skeleton for an oscillator, it's an iterator (cause of the __iter__ and __next__) that with the getters and setters to change the phase, amplitude and frequency without altering the values that were set at the point of instantiation, such as when the note is pressed.
So for example the property ._freq represents the fundamental frequency of the oscillator, this doesn't change, and the property ._f represents the altered frequency which is the frequency of the returned wave, obtained on calling __next__.
The idea is that when a key is pressed __iter__ is called once, and the __next__ is called as long as the key is held.
Also, a static method squish_val has been added, this is to bring the oscillator output into a given range.
Sine Oscillator, Revisited 🌇
Now we'll extend the Oscillator abstract base class to recreate the sine oscillator with all the required functionality.
class SineOscillator(Oscillator):
def _post_freq_set(self):
self._step = (2 * math.pi * self._f) / self._sample_rate
def _post_phase_set(self):
self._p = (self._p / 360) * 2 * math.pi
def _initialize_osc(self):
self._i = 0
def __next__(self):
val = math.sin(self._i + self._p)
self._i = self._i + self._step
if self._wave_range is not (-1, 1):
val = self.squish_val(val, *self._wave_range)
return val * self._a
Yay. We have a sin oscillator in 17 lines rather than 4. I know, I know, trust me this will all make sense when we get to modulation.
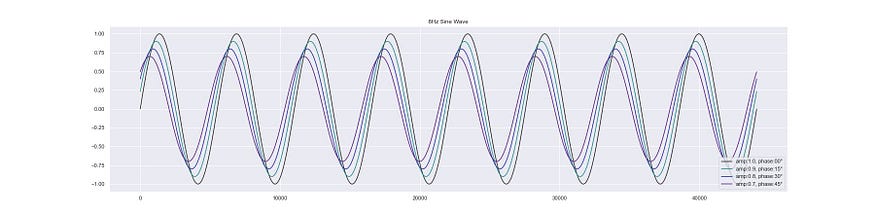
4, 8 Hz sine waves with different parameters.
All the plots in this post are at infrasonic frequencies, cause at higher frequencies the waveform is too condensed to be properly visible on a plot, so I have recorded snippets of waveforms so you can hear what they sound like.
Here's ☝️ how the sine wave sounds, the one second long sample is playing a C4, E4 and G4 in sequence (the notes of a C Major chord).
Beyond sines, squares 🟪
Sine waves are nice but are kinda bland on their own, your waves gotta have more character. A quick way to get another wave is to threshold the sinewave at some level and then return a high or a low value depending on which side of the threshold the sine value is.
class SquareOscillator(SineOscillator):
def __init__(self, freq=440, phase=0, amp=1, \
sample_rate=44_100, wave_range=(-1, 1), threshold=0):
super().__init__(freq, phase, amp, sample_rate, wave_range)
self.threshold = threshold
def __next__(self):
val = math.sin(self._i + self._p)
self._i = self._i + self._step
if val < self.threshold:
val = self._wave_range[0]
else:
val = self._wave_range[1]
return val * self._a
The above class extends SineOscillator to give us a square wave oscillator with the same set of functionalities.

4, 8 Hz square waves with different parameters.
Et voilà! We have a square wave. Pretty simple, no!? Here's 👇 how it sounds, it's kinda harsh so probably reduce your volume.
Sawteeth for sounds 🪚
I wasn't gonna add more than the sine oscillator at first, and this was meant to be a single post but then I got carried away; so, here's another oscillator, the SawtoothOscillator.
class SawtoothOscillator(Oscillator):
def _post_freq_set(self):
self._period = self._sample_rate / self._f
self._post_phase_set
def _post_phase_set(self):
self._p = ((self._p + 90)/ 360) * self._period
def _initialize_osc(self):
self._i = 0
def __next__(self):
div = (self._i + self._p )/self._period
val = 2 * (div - math.floor(0.5 + div))
self._i = self._i + 1
if self._wave_range is not (-1, 1):
val = self.squish_val(val, *self._wave_range)
return val * self._a
It isn't related to the sine oscillator like the square is.
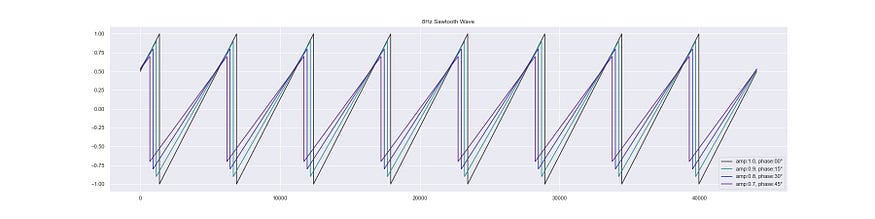
4, 8 Hz sawtooth waves with different parameters.
This is what the sawtooth sounds like, it's less harsher than the square.
Triangles are my favourite shape…
The Oscillator ABC makes it pretty easy to create new oscillators, let's make the final one, a triangle oscillator.
class TriangleOscillator(SawtoothOscillator):
def __next__(self):
div = (self._i + self._p)/self._period
val = 2 * (div - math.floor(0.5 + div))
val = (abs(val) - 0.5) * 2
self._i = self._i + 1
if self._wave_range is not (-1, 1):
val = self.squish_val(val, *self._wave_range)
return val * self._a
The triangle wave is basically just the absolute value of the sawtooth wave, so it's different by only a single line, the other stuff is just so that the range of the wave is between -1 and1.

4, 8 Hz triangle waves with different parameters.
Here's what it sounds like, kinda like a slightly dirty sine wave.
We now have 4 different oscillators at our disposal, the things we can now do, the sounds we can now make…
Seeing The Waves Differently 👁
All the earlier plots of the waveforms have been in the time domain, which basically means that they were amplitude vs time plots of the waves, to understand why pure waves are kinda bland we gotta view them in the frequency domain.
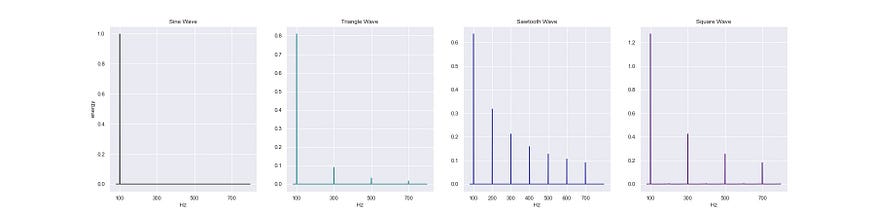
100 Hz signals of the four waves in the frequency domain.
Sine wave is known as a pure wave cause it has no harmonics (integer multiples of the fundamental frequency) besides the fundamental frequency, in the amplitude vs frequency graph, all we can see is a single spike at 100 Hz which is the fundamental frequency of the wave.
In contrast to the sine wave, the triangle and the square have odd harmonic frequencies (odd multiples of the fundamental frequency) but with different energy distributions, and sawtooth has both odd and even harmonics.
These collection of frequencies is what lends a wave it's unique sound, it's timbre.
On observing the graphs, it might seem that the other waves can be reconstructed from combinations of sine waves and this is true, it's called Additive Synthesis!
Adding The Waves 🌊
In a synthesizer multiple oscillators tend to be used with each other, i.e. instead of just using a single oscillator we can mix the output of multiple oscillators to get a more complex sound.
class WaveAdder:
def __init__(self, *oscillators):
self.oscillators = oscillators
self.n = len(oscillators)
def __iter__(self):
[iter(osc) for osc in self.oscillators]
return self
def __next__(self):
return sum(next(osc) for osc in self.oscillators) / self.n
This simple class will allow us to mix the output of any number of oscillators that have been initialized with different parameters.
Here's the sum of two sine waves:

Sum of two sine waves.
Here's something a bit more crazier, the sum of waves from all the oscillators, see the frequencies, the wave has a lot more character.

Sum of all the 4 waves at different frequencies.
Saving the Waves
To save the generated sounds onto your disk to listen to them, you can use this function:
import numpy as np
from scipy.io import wavfile
def wave_to_file(wav, wav2=None, fname="temp.wav", amp=0.1, sample_rate=44100):
wav = np.array(wav)
wav = np.int16(wav * amp * (2**15 - 1))
if wav2 is not None:
wav2 = np.array(wav2)
wav2 = np.int16(wav2 * amp * (2 ** 15 - 1))
wav = np.stack([wav, wav2]).T
wavfile.write(fname, sample_rate, wav)
The arg wav2 can be used to write stereo audio to the .wav file. You can then use it to generate and save the wave using some code like this:
gen = WaveAdder(
SineOscillator(freq=440),
TriangleOscillator(freq=220, amp=0.8),
SawtoothOscillator(freq=110, amp=0.6),
SquareOscillator(freq=55, amp=0.4),
)iter(gen)
wav = [next(gen) for _ in range(44100 * 4)] ### 4 Seconds
wave_to_file(wav, fname="prelude_one.wav")
The code above generates the wave in the (non subtitled) Introduction.
Let's Hear Some Waves 🎧
Adding the waves gives us really strange looking waveforms, but since those have been infrasonic for visualization purposes, here's some audio samples of mixed waves, use earphones or headphones if you can cause there are low frequencies and the left and right play different tones.
Here's ☝️ one that kind of has an operating theater kinda feel to it, with a binaural beats thing also going on.
This 👆 is an A minor 6 with a 3Hz oscillation cause of the frequency difference in the bass.
And finally to end on a happy note, here's an arpeggiated C Major 7 with a hemiola in the bass.
Conclusion
I'll be adding all the code from these posts to this repo, the end result should be a playable synth.🤞
The code used for generating the samples and the plots are in this notebook, you can play around with the sounds, ⚠️ it's a time sink.
Link to the second post on Modulators.
Link to the third post on Controllers.
Thanks for reading. ✌️
Comments
Loading comments…