
Hi everyone, in my last article we examined the Greedy Algorithm, and used it in order to find a path from a starting to a final (target) point. The Greedy algorithm was the first heuristic algorithm we have talked about. Today, we are going to talk about another search algorithm, called the *Uniform Cost Search (UCS) *algorithm, covering the following topics:
1. Introduction
2. Pseudocode
3. Pen and Paper Example
4. Python implementation
5. Example
6. Conclusion
So let the party begin…
Introduction
As we already mentioned in the past, search algorithms like Breadth-First Search, Depth First Search, the Greedy algorithm, and of course the UCS algorithm, are used to find a solution in a graph. The graph represents the given problem, in which each vertex (node) of the graph represents a state of the problem and each edge represents a valid action that takes us from one state (vertex) to the other. If you want to learn more about graphs follow the link below:
Graph Data Structure — Theory and Python Implementation
In contrast to BFS and DFS algorithms that don't take into consideration neither the cost between two nodes nor any heuristic value, the Greedy algorithm uses a heuristic value, such as the Manhattan distance, or the Euclidean distance to estimate the distance from the current node to the target node. On the other hand, the UCS algorithm uses the path's cost from the initial node to the current node as the extension criterion**. Starting from the initial state (starting node), the UCS algorithm, in each step chooses the node that is **closer **to the initial node. When the algorithm finds the solution, returns the path from the initial state to the final state. The UCS algorithm is characterized as complete, as it always returns a solution if exists. Moreover, the UCS algorithm guarantees the optimum solution.
Pseudocode
The UCS algorithm takes as inputs the graph along with the starting and the destination nodes and returns the optimum path between these nodes if exists. Similar to the Greedy algorithm, the UCS algorithm uses two lists, the *opened *and the *closed *list. The first list contains the nodes that are possible to be selected and the closed list contained the nodes that have already been selected. Firstly, the first node (initial state) is appended to the opened list (initialization phase). In each step, the node (selected node)with the smallest distance value is removed from the opened list and is appended to the closed list. For each child of the selected node, the algorithm calculates the distance from the first node to this. If the child does not exist in both lists or is in the opened list but with a bigger distance value from the initial node, then the child is appended in the opened list in the position of the corresponding node. The whole process is terminated when a solution is found, or the opened list be empty. The latter situation means that there is not a possible solution to the related problem. The pseudocode of the UCS algorithm is the following:
1. function UCS(Graph, start, target):
2. Add the starting node to the opened list. The node has
3. has zero distance value from itself
4. while True:
5. if opened is empty:
6. break # No solution found
7. selecte_node = remove from opened list, the node with
8. the minimun distance value
9. if selected_node == target:
10. calculate path
11. return path
12. add selected_node to closed list
13. new_nodes = get the children of selected_node
14. if the selected node has children:
15. for each child in children:
16. calculate the distance value of child
17. if child not in closed and opened lists:
18. child.parent = selected_node
19. add the child to opened list
20. else if child in opened list:
21. if the distance value of child is lower than
22. the corresponding node in opened list:
23. child.parent = selected_node
24. add the child to opened list
Pen and Paper example
Before implementing the UCS algorithm in Python, let's see an example to have a better understanding and intuition about the whole algorithmic procedure. We are going to use the example we used in Dijkstra's algorithm. We suppose that we have a graph representing a roadmap of a country, in which there are six cities (vertices — nodes) and a couple of edges connecting these cities. The graph has the following form:
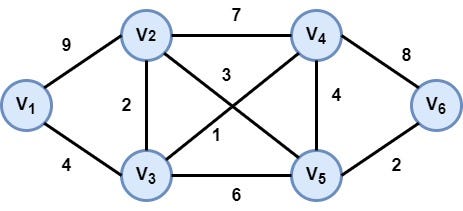 Graph that models the roadmap of the problem
Graph that models the roadmap of the problem
Our target is to go from the city (node) V1 to V6 following the path with the smallest cost (shortest path). Let's execute the UCS algorithm:
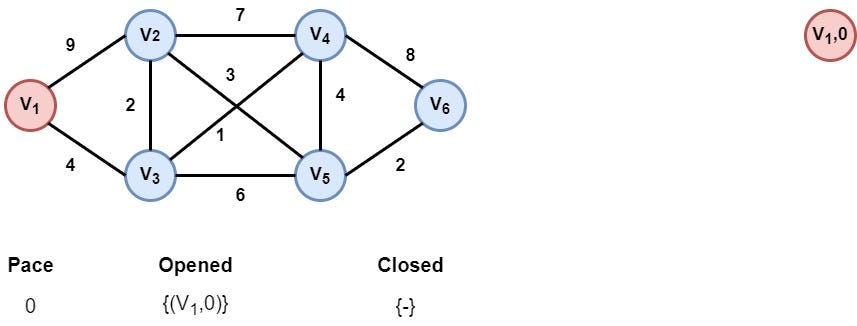
Step 1: Initialization
The first node V1 (initial state) of the graph is appended to the opened list. The distance of this node from itself is zero.
Step 2: Node V1 is selected
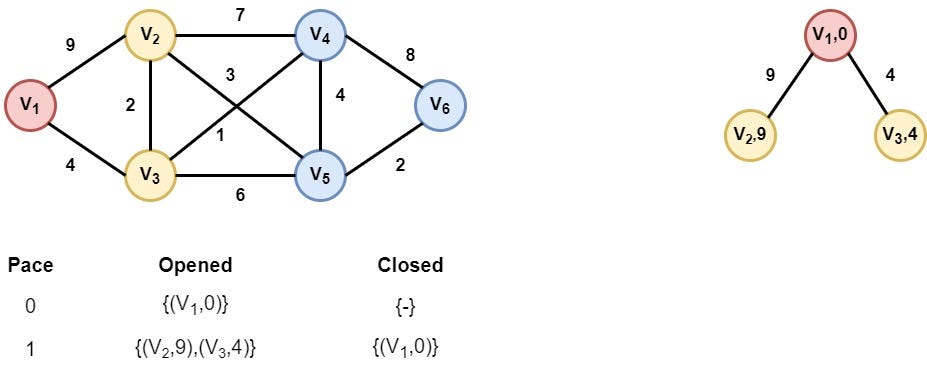
The V1 is selected as it is the only node in the opened list. Its children V2 and V3 are appended in the opened list after the distance calculation from node V1.
Step 3: Node V3 is selected
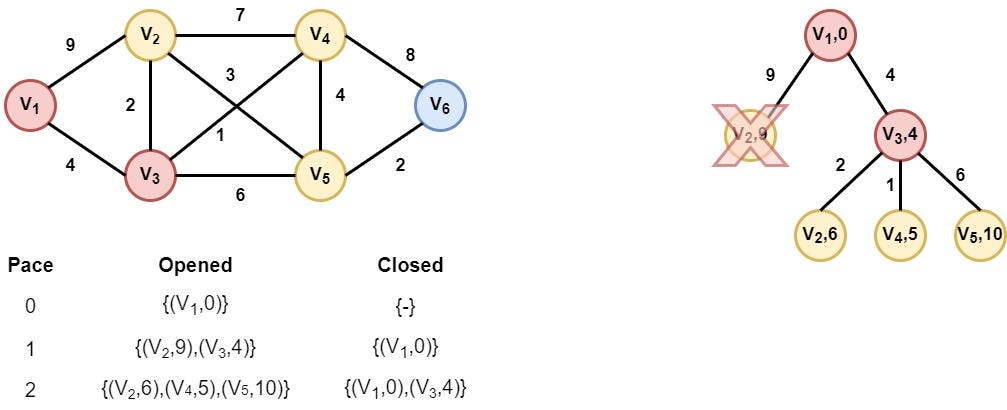
Node V3 is selected as it has the smallest distance value. As we can see, extending the node V3 we find the node V2 with a smaller distance value. So we replace node (V2,9) with the new node (V2,6).
Step 4: Node V4 is selected
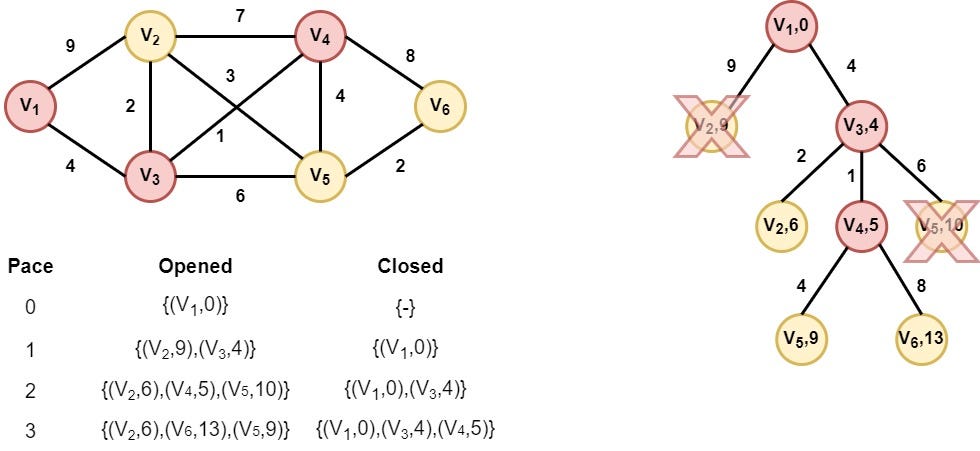
Node V4 is selected as it has the smallest distance value. In this step, we find a better distance value for node V5, so we replace the node (V5, 10) with node (V5, 9).
Step 5: Node V2 is selected

Node V2 is selected as it has the smallest distance value. However, none of its children is appended in the opened list, as nodes V3 and V4 are already inserted in the closed list and the algorithm doesn't find a better distance value for node V5.
Step 6: Node V5 is selected

Node V2 is selected as it has the smallest distance value. A better path to node V6 is found in this step. So, we replace the old node (V6, 13) with node (V6, 11)
Step 7: Node V6 is selected
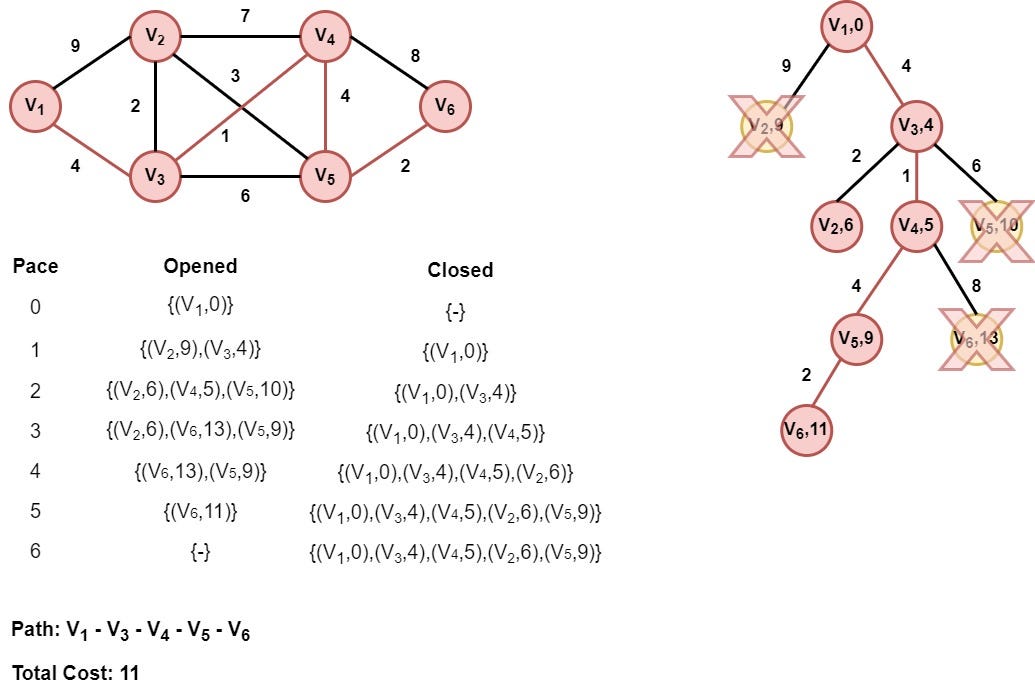
Node V6 (target node) is selected. So the algorithm returns the path from node V1 to node V6 with cost 11, which constitutes the best solution.
Python implementation
Having understood the algorithmic procedure of the UCS algorithm is time to implement it in Python. We are going to extend the code from the Graphs article for this purpose.
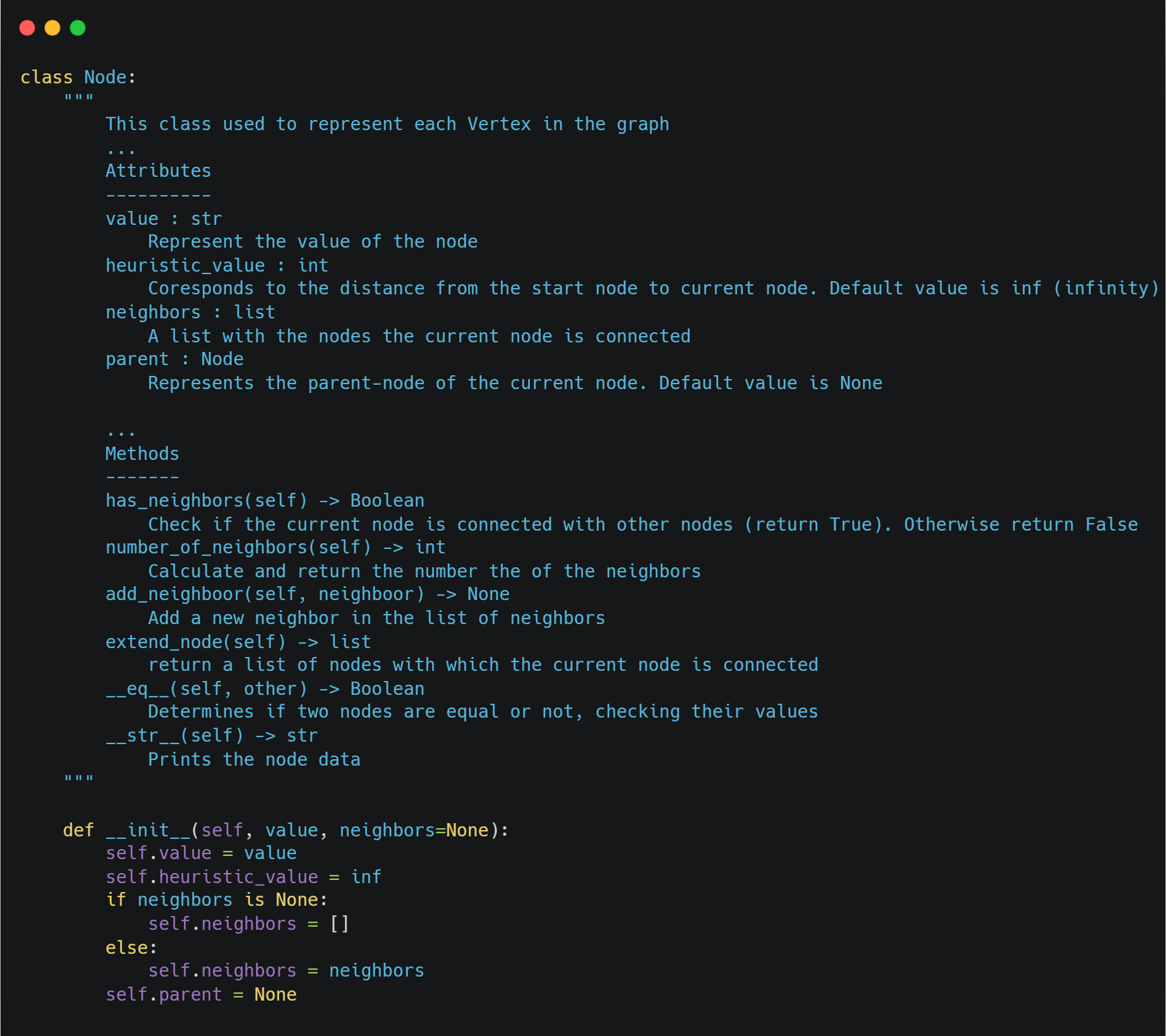
First, we create the class *Node *that represents each node of the graph. This class has a couple of attributes such as the heuristic value that corresponds to the distance from the initial node. An overview of the *Node *class is the following.
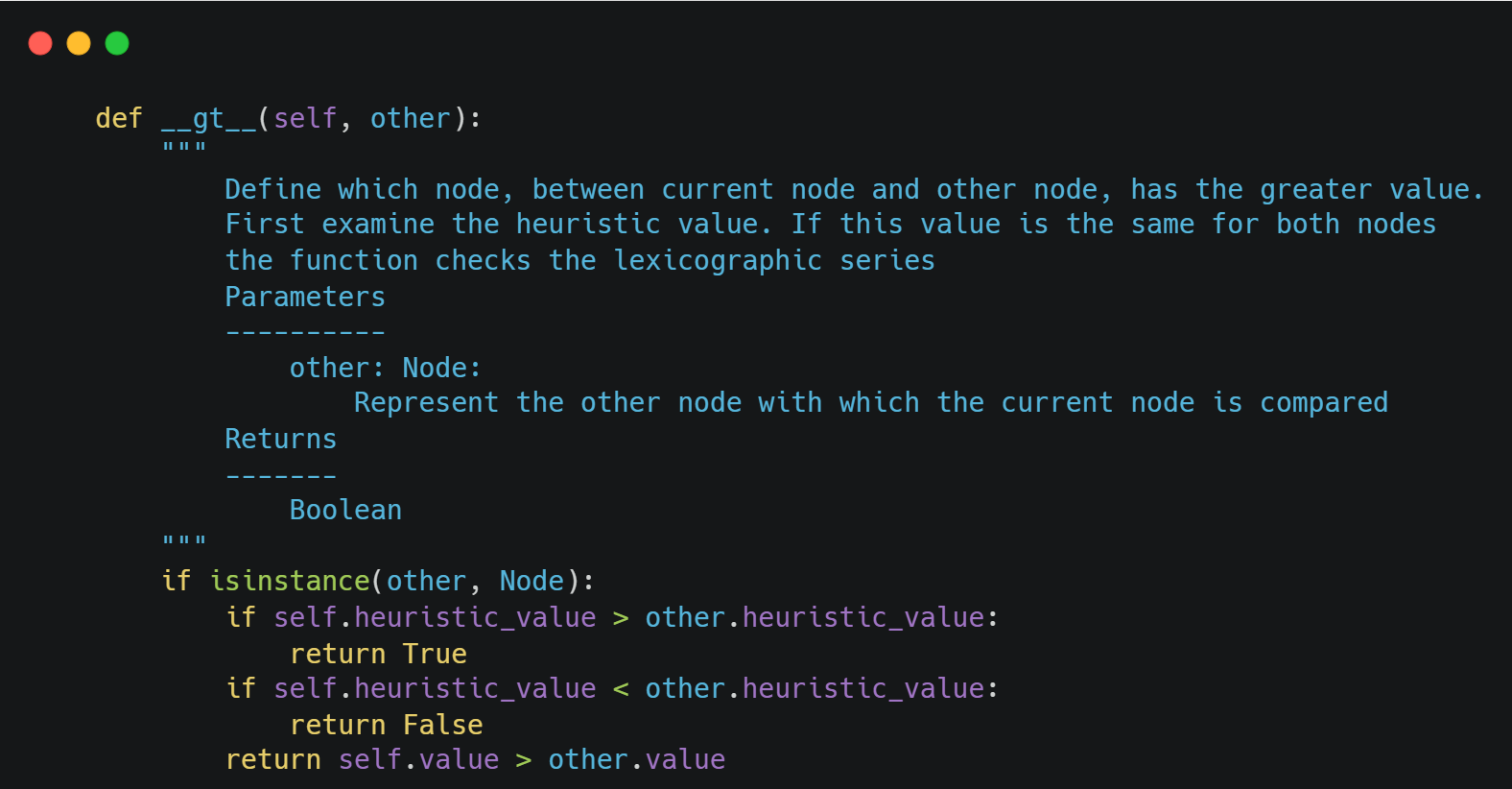
We compare the nodes according to their heuristic value (distance from the initial node). So, we implement the magic of the dunder method gt(), which defines the way the nodes are compared to each other.
The main class of the algorithm is the *UCS *class that represents the UCS algorithm. This class has a couple of attributes, such as the *graph *which represents the model of the problem, the *opened *and *closed *lists, etc. An overview of the class is the following:

Learn How to Use the gt() Method in Python
To calculate the distance from the initial node to the current node we use the following method:

Finally, the core algorithm is the *search() *method that represents the whole algorithmic procedure.

Example
Now, we are ready to test our implementation using the example above as the input of the algorithm. Remember that the search space of our example is the following:

We can model the graph above as follows:

As we can see, we have the same results. Remember, that the UCS algorithm always returns the optimum solution, so this path is the shortest path as we also have calculated in the article about Dijkstra's algorithm. An Introduction to Dijkstra's Algorithm: Theory and Python Implementation
You can see and download the whole code here.
Conclusion
In this article, we had the opportunity to talk about the UCS Algorithm, to find the best solution from an initial (starting) node to the target node. In contrast to the Greedy algorithm that uses a heuristic value, such as the Manhattan distance, to estimate the distance to the target node, the UCS algorithm (like Dijkstra's algorithm) uses the distance from the initial node to select the next node in the path. In the next article, we will talk about the well-known A algorithm to find the optimum solution to a given graph problem. Until then, keep learning and keep coding.
If you want to read more articles like this one, regarding Algorithms, Data Structures, Data Science, and Machine Learning follow me on Medium, LinkedIn, and Twitter.
Learn more about Search Algorithms
An Introduction to A* Algorithm in Python
Solve Maze Using Breadth-First Search (BFS) Algorithm in Python
How to Solve Sudoku with Depth-first Search Algorithm (DFS) in Python
Comments
Loading comments…