Photo by Mark Rabe on Unsplash
Introduction
Algorithms & Data Structures interviews are notoriously difficult. Coming up with an optimal approach to a problem is already time-consuming. So, if you become stuck on the implementation, you may not even finish the problem! As a result, understanding how to use each of the core data structures and knowing the Python-specific caveats about them will make the implementation seamless.
Agenda
Stack
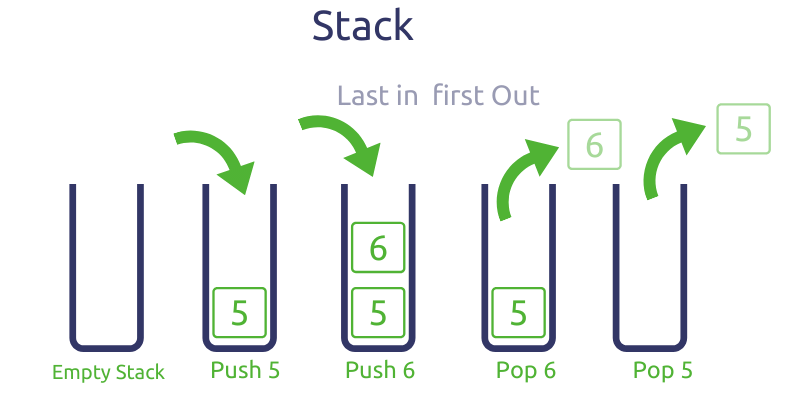
Photo on holycoders
To recap, a stack allows us to push and pop elements of the top, and get the top element in O(1) time. Though there isn’t an explicit stack class in Python, we can use a list instead.
We can use append and pop to add and remove elements off the end in amortized O(1) time (Time Complexity). Python lists are implemented as dynamic arrays. Once the array is full, Python will allocate more memory for a larger array and copy the old elements to it. Since this reallocation doesn’t happen too often, append will still be O(1) in most cases.
Also, we can index into the list with -1 to get the last element in a list. Basically, the end of the list will be the “top of the stack”.
Queue
Photo by Adrien Delforge on Unsplash
Using a stack is simple, but what if we wanted to process data in FIFO (First In First Out) order. In the collections package, Python provides deque, a double-ended queue class. With deque, we can insert and remove from both ends in O(1) time. The deque constructor takes in an iterable: we can pass in an empty list to create an empty deque.
from collections import deque
queue = deque([])
The main methods are append, appendleft, pop and popleft. As the names suggest, append and pop will add and remove elements from the end, whereas appendleft and popleft do the same at the front. In order to emulate a queue, we add from one side and remove from the other.
If you noticed, we can also use deque to emulate a stack: we add and remove from the same side.
On a different note, I want to highlight a common mistake in interviews: using lists as queues.
Let’s consider 2 ways we can use lists as queues.
We can add to the front of the list and remove from the end. This requires using insert at index 0 and pop.
queue = [2,3,4,5]
# add 1 at index 0, [1,2,3,4,5]
queue.insert(0, 1), [1,2,3,4,5]
# pop 5 from the end, [1,2,3,4]
element = queue.pop()
The problem is that inserting an element at the front of a list is O(N), since all the other elements must be shifted to the right (Time Complexity).
Let’s say instead we decided to add at the end and remove from the front.
queue = [5,4,3,2]
# add 1 to the end, [5,4,3,2,1]
queue.append(1)
# pop 5 from the front, [4,3,2,1]
element = queue.pop(0)
The problem still remains, since popping from the front of the list will be O(N) as everything to the right must shift to the left.
Even though using lists as queues is fine if the lists are relatively small, using them over the more efficient deque in an interview setting where time complexity is important is not ideal.
Priority Queue
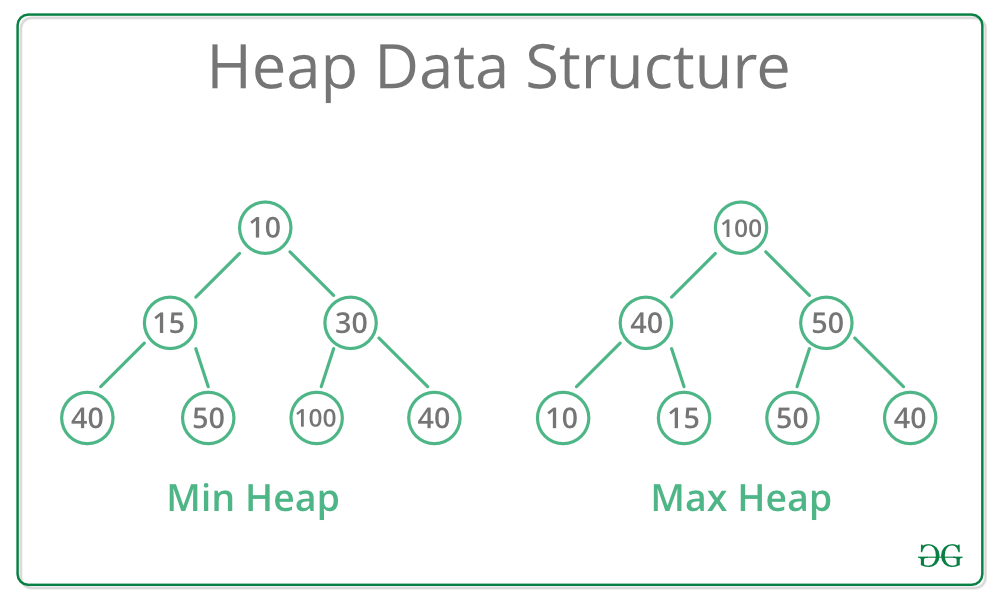Photo on geeksforgeeks
Similar to stacks, there is no explicit class to create a priority queue or a heap in Python. Instead, we have heapq, a collection of methods that allows us to use lists as heaps.
Allow me to demonstrate.
import heapq
# create a new 'heap'. it is really just a list
heap = []
We can add elements to our heap with heapq.heappush and pop elements out of our heap with heapq.heappop.
# push the value 1 into the heap
heapq.heappush(heap, 1)
# pop the value on top of the heap: 1. The heap is now empty
element = heapq.heappop(heap)
heapq.heappush and heapq.heappop will maintain the min-heap invariant in the list that we use as a heap.
Here is what I mean:
heap = []
numbers = [9,2,4,1,3,11]
k = 3
ksmallest = []
for number in numbers:
heapq.heappush(heap, number)
for i in range(k):
ksmallest.append(heapq.heappop(heap))
# ksmallest is [1,2,3]
print(ksmallest)
If I were to push all the elements in numbers into heap and pop out 3 times, I would get the 3 smallest elements, or [1,2,3]. There is no “setting” that tells the heapq functions to treat our heap as a max-heap: the functions “assume” that the passed in heap is a min-heap and only provide the expected results if it is.
How can I make a list of elements into a min-heap?
As shown above, one approach is to make an additional empty list and push the elements into that list with heapq.heappush. The time complexity of this approach is O(NlogN) where N is the number of elements in the list.
A more efficient approach is to use heapq.heapify. Given a list, this function will swap its elements in place to make the list a min-heap. Moreover, heapq.heapify only takes O(N) time.
But… What do I do if I want a max-heap?
As previously stated, we cannot directly use a max-heap with heapq. Instead, we can try to invert our elements in the min-heap so that the larger elements get popped out first.
For example, say I have a list of numbers, and I wanted the K largest numbers. To begin, we can invert the numbers by multiplying by -1. The numbers that were the largest are now the smallest. We can now turn this collection of numbers into a min-heap. When we pop our inverted numbers from the heap, we simply multiply by -1 again to get our initial number back.
In situations where you need a max-heap, consider how you can reverse the order of the elements, turning the largest elements into the smallest.
Wait… How do I compare across multiple fields?
Suppose we had the age and height (in inches) of students stored in a list.
# each entry is a tuple (age, height)
students = [(12,54),(18,78),(18,62),(17,67),(16,67),(21, 76)]
Let’s say we wanted to get the K youngest students, and if two students had the same age, let’s consider the one who is shorter to be younger. Unfortunately, there is no way for us to use a custom comparator function to handle cases where two students have the same age. Instead, we can use tuples to allow the heapq functions to compare multiple fields.
To provide an example, consider the students at indices 0 and 1. Since, student 0’s age, 12, is less than student 1’s, 18, student 0 will be considered smaller and will be closer to the top of the heap than student 1.
Let’s now consider student 1 and student 2. Since both of their ages are the same, the heapq functions will compare the next field in the tuple, which is height. Student 2 has a smaller height, so student 2 will be considered smaller and will be closer to the top.
If you need to compare against multiple fields to find out which element is smaller or bigger, consider having the heap’s elements be tuples.
Dictionary
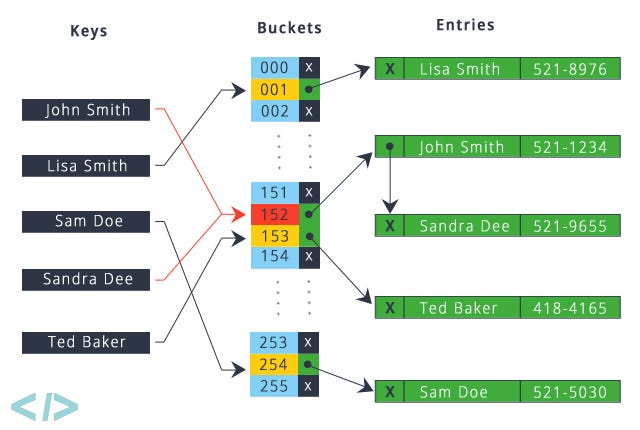
Photo on codenuclear
Dictionaries are the Python equivalent to Hash Maps and are an overpowered data structure. In most cases, we can look up, add, delete and update keys in O(1) time. Let’s go over the basics of dictionaries.
# empty dict
d = {}
# dict with some keys and values
d = {
"name": "James",
"age": 29
5: 29.3
}
When declaring a dictionary, we put the keys on the left and values on the right, separated by a colon. In Python, the keys of a dictionary can only be hashable values, like int, str, tuple, and more (Hashable Objects). In addition, a dictionary can have keys and values of multiple types as shown above.
We can also add, update and delete keys with [].
# add key "numbers" to d
d["numbers"] = [1,2,4,12]
# update key "numbers" of d
d["numbers"] = [1,3,6,18]
# delete key "numbers" of d
del d["numbers"]
We can also easily check if a key is in a dictionary with in.
doesNumbersExist = "numbers" in d
Python also provides a nice way of iterating over the keys inside a dictionary.
d = {"a": 0, "b": 5, "c": 6, "d": 7, "e": 11, "f": 19}
# iterate over each key in d
for key in d:
print(d[key])
When you are iterating over keys in this manner, remember that you cannot add new keys or delete any existing keys, as this will result in an error.
What happens if I try to access a key which doesn’t exist?
d = {"a": 0, "b": 7}
c_count = d["c"] # KeyError: 'c'
In the above snippet, “c” does not exist. We will get a KeyError when we run the code. As a result, in many situations, we need to check if the key exists in a dictionary before we try to access it.
Although this check is simple, it can be a hassle in an interview if we need to do it many times. Alternatively, if we use collections.defaultdict, there is no need for this check. defaultdict operates in the same way as a dictionary in nearly all aspects except for handling missing keys. When accessing keys that don’t exist, defaultdict automatically sets a default value for them. The factory function to create the default value can be passed in the constructor of defaultdict.
We can also pass in a lambda as the factory function to return custom default values. Let’s say for our default value we return the tuple (0, 0).
pair_dict = defaultdict(lambda: (0,0))
# prints True
print(pair_dict['point'] == (0,0))
Using a defaultdict can help reduce the clutter in your code, speeding up your implementation.
Conclusion
The main goal of this article was to explain the core data structures in Python, and to make you aware of their caveats so you can kill the implementation portion of your interview! I hope you walked away learning something new and thank you for reading!