Hello everyone! Today we will talk about what is stereo camera and how we are using it for computer vision. By using the code I wrote for you, I will explain how we are calibrating the camera for stereo cameras and calculate a disparity map. I won't go into mathematical details, you can read some OpenCV documents for that. Let's start!
This is the magic we'll cover today!
The reason we can perceive the depth is our beautifully aligned eyes. If you noticed, when we look close objects with one eye, we'll see a difference between both perspectives. But when you look something far away, like mountains or buildings kilometers away, you won't see a difference. These differences are automatically processed in our brain and we can perceive the depth! Animals that have eyes aligned far right and far left can't perceive depth because they don't have common perspectives, instead they have a wide-angle perspective. Some of them, like ducks, shake their heads or run fast to perceive depth, it's called structure from motion. We won't cover this concept, for now, let's focus on a system like our eyes.
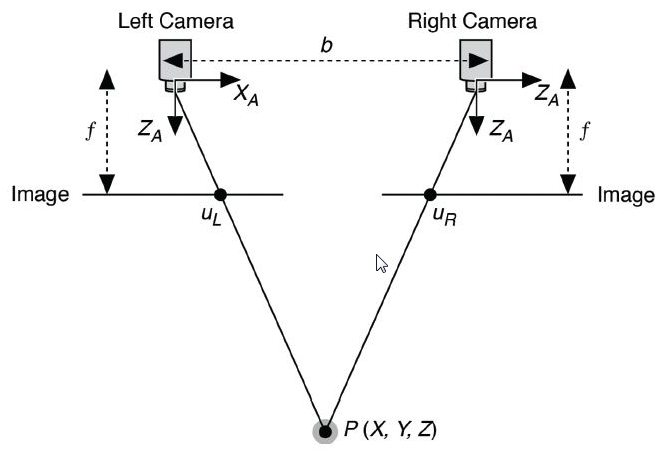Simplified stereo vision. You see how an object P is observed from two cameras. The object's position is different in both images.
If two cameras aligned vertically, the observed object will be in the same coordinates vertically(same column in the images), so we can only focus on x coordinates to calculate the depth since close objects will have a higher difference in the x-axis. But to achieve that, we need to calibrate the cameras to fix lens distortions. After the calibration, we need to rectify the system. Rectification is basically calibration between two cameras. If we calibrate and rectify our stereo cameras well, two objects will be on the same y-axis and observed point P(x,y) can be found in the same row in the image, P1(x1,y) for the first camera and P2(x2,y) for the second camera. From there, it's the only difference between the pixels and depth calculations.
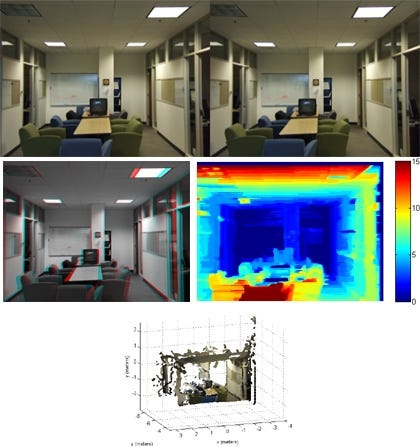Respectively, upper left and right images are rectified left/right camera images, lower left is their combination to show the difference, lower right is the depth map.
First, mount the stereo cameras to a solid object(ruler, wood or hard plastic materials, etc.) so that the calibration and rectification parameters will work properly. If you have Intel Realsense or zed camera, for example, you can skip all the parts because Realsense has auto-calibration and zed is already calibrated as factory-default. The next step is the calibration of both cameras separately. You can follow my calibration guide for that, it's highly recommended for the next steps. Stereo cameras required the single calibration first since rectification requires these parameters. Use a chessboard image for the calibration and use at least 20 images for good calculation.
Example of left and right images. Be careful about shoot sync, we'll use these for rectification as well. In rectification, even a little difference may affect the result.
These images will give us the information we need for the cameras. You shouldn't move and get sync images for better calibration. You can use grab & retrieve functions to get a much closer timestamp. For taking images, you can use this code and for the calibration, you can use this one. About the codes:
-
Stereo calibration: Camera calibration for stereo camera set.
-
Stereo rectification: Finding a rotation and translation to make them aligned in the y-axis so that each point observed by these cameras will be in the same column in the images from each camera.
OpenCV stereo calibration function:
ret, K1, D1, K2, D2, R, T, E, F = cv2.stereoCalibrate(objp, leftp, rightp, K1, D1, K2, D2, image_size, criteria, flag)
We should care about the flags of this function. Let's cover those:
-
CV_CALIB_FIX_INTRINSIC: K and D matrices will be fixed. It is the default flag. If you calibrated your camera well, you can fix them so you'll only get the rectification matrices.
-
CV_CALIB_USE_INTRINSIC_GUESS: K and D matrices will be optimized. For this calculation, you should give well-calibrated matrices so that the result will be better(possibly).
-
CV_CALIB_FIX_PRINCIPAL_POINT: Fix the reference point in the K matrix.
-
CV_CALIB_FIX_FOCAL_LENGTH: Fix the focal length in the K matrix.
-
CV_CALIB_FIX_ASPECT_RATIO: Fixing the aspect ratio.
-
CV_CALIB_SAME_FOCAL_LENGTH: Calibrate the focal length and set Fx and Fy the same calibrated result. I am not familiar with this one but I am sure it's required for specific stereo setups.
-
CV_CALIB_ZERO_TANGENT_DIST: Remove the distortions.
-
CV_CALIB_FIX_K1, …, CV_CALIB_FIX_K6: Remove distortion K1 to K6. Really important for experimentation. I am not familiar with the math behind those but the experiments I've made on these helped me a lot.
R, T, E, F coefficients in the result give us the relation between two cameras and we'll use them for rectification:
R1, R2, P1, P2, Q, roi_left, roi_right = cv2.stereoRectify(K1, D1, K2, D2, image_size, R, T, flags=cv2.CALIB_ZERO_DISPARITY, alpha=0.9)
In this function, we have only one flag, CALIB_ZERO_DISPARITY and it's used to match the y-axis between the images. The alpha value is used to work on the black parts after the transformation since images will rotate and our size won't change so that some of the images will be black and our original image will be much smaller. I set the value for my camera. The options are:
-
alpha=-1 -> Let OpenCV optimize black parts.
-
alpha= 0 -> Rotate and cut the image so that there will be no black parts. This option cuts the image so badly most of the time, that you won't have a decent high-quality image but worth to try.
-
alpha= 1 -> Make the transform but don't cut anything.
-
alpha=experimental-> Sometimes nothing works for you. This means that you should experiment with the values. If it's okay for you to have some black part, but the high quality image, you can work on the alpha value. I found the best at 0.9756 for my camera, so don't lose hope :)
R and P matrices are called rotation and projection matrices. R1 and P1 give the rotation and position from first(left) to the second(right) camera. R2 and P2 are from second to first. Q matrix is required to get depth map from disparity map. Includes the distance between cameras, focal length etc. for depth map processing. When the depth values calculated, don't forget that you'll get the coordinates in the same unit you worked with calibration. There are a lot of parameters so it's better to double-check everything.
For the results, we should check our test code. If we read the main part, we'll see that we use the rectification with undistortion:
leftMapX, leftMapY = cv2.initUndistortRectifyMap(K1, D1, R1, P1, (width, height), cv2.CV_32FC1)
left_rectified = cv2.remap(leftFrame, leftMapX, leftMapY, cv2.INTER_LINEAR, cv2.BORDER_CONSTANT)
rightMapX, rightMapY = cv2.initUndistortRectifyMap(K2, D2, R2, P2, (width, height), cv2.CV_32FC1)
right_rectified = cv2.remap(rightFrame, rightMapX, rightMapY, cv2.INTER_LINEAR, cv2.BORDER_CONSTANT)
It means that initUndistortRectifyMap function both undistorts and rectifies the images. For the left camera, we use K1(camera matrix) and D1(distortion matrix) to undistort and R1(left to right rotation) and P1(left to right projection matrix) to rectify. After the transformation is given to remap, we'll get the rectified images. We'll to the same one for the right camera and the first part is done! Summarizing the process:
That's all about stereo calibration and rectification. We'll cover the disparity map calculation in the next blog!
Resources: