
Hi everyone, one of my first articles in medium talked about Search Algorithms. These algorithms are applied in graphs, which model a given problem, creating the search space of the problem. They search in the search space (graph) to find the best or at least a quite efficient solution. Particularly, we have implemented the Breadth-First Search (BFS) and the Depth First Search (DFS) to solve the maze problem and a sudoku puzzle respectively. Today we are going to talk about the Greedy algorithm. More specifically, we will talk about the following topics:
- Introduction
- Pseudocode
- Pen and Paper Example
- Python implementation
- Example
- Conclusion
We have a lot of stuff to cover, so let’s get started.
Introduction
Search Algorithms are used to find a solution to a given problem, that can be modeled as a Graph. If you want to learn more about graphs, please read the related article. Every node in the graph represents a state of the problem and each edge between two nodes represents a valid action that drives us from one state (node) to the other. Each Search Algorithm starts from a node (initial state — node) searching the final state node that represents a solution for the given problem. Search Algorithms are divided into two main categories. The first category contains the so-called “blind” algorithms, that don’t take into account the cost between the nodes. Breadth-First Search and Depth First Search algorithms we talked about in previous articles are in this category. The algorithms in the second category execute the heuristic search. The Greedy algorithm belongs to the latter category.
Graph Data Structure — Theory and Python Implementation
Heuristic search methods try to find the optimal solution in a reasonable time for a given problem. In contrast to “blind” search methods and algorithms that use brute force to find a solution, the heuristic algorithms use information about the distance between nodes and evaluate the cost for each possible path. To do that, heuristic algorithms use a heuristic method that calculates that cost. Be careful, the heuristic value that is calculated by the heuristic method does not have to exceed the real distance of the nodes. For example, if in a graph the distance (weight) of two nodes is 10, then the heuristic value does not have to exceed this value. Otherwise, the algorithm will produce wrong results.
A well-known heuristic method is the Manhattan Distance. The Manhattan Distance is the sum of the absolute difference between two points. We can calculate the manhattan distance using the following formula:
manhattan((x1, y1), (x2, y2)) = |x1 — x2| + |y1 — y2|
where (x1,y1) is the coordinates of the first node and (x2, y2) the coordinates of the second node respectively. We can use other heuristic methods like Euclidean Distance, etc.
As we mentioned earlier, the Greedy algorithm is a heuristic algorithm. We are going to use the Manhattan Distance as the heuristic function in this tutorial. The Greedy algorithm starts from a node (initial state), and in each step, chooses the node with the minimum heuristic value, which is the most promising for the optimum solution. When it finds the solution, return the path from the initial state to the final state. The Greedy algorithm is characterized as complete, as it always returns a solution if exists. However, this algorithm does not guarantee the optimum solution.
Pseudocode
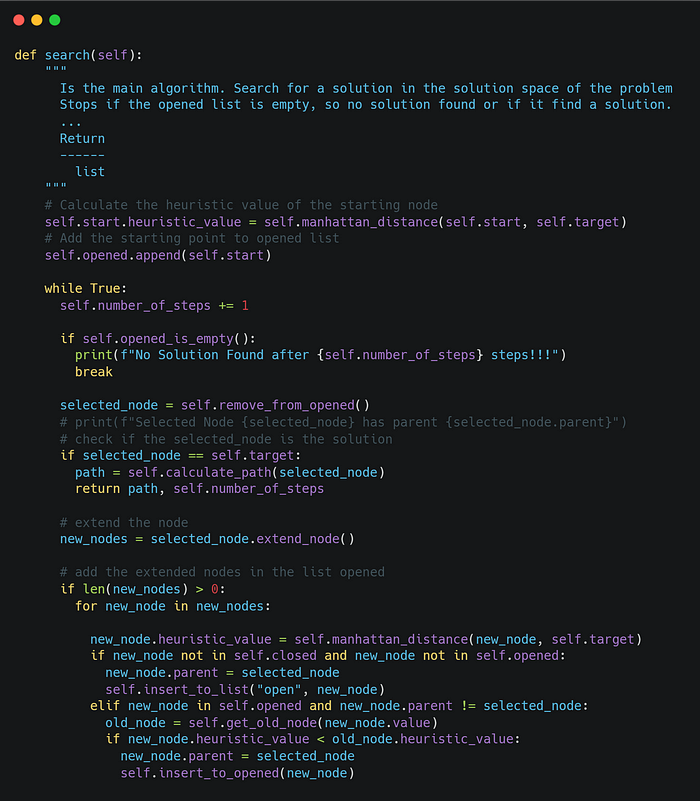
The Greedy algorithm takes a graph as an input along with the starting and the destination point and returns a path if exists, not necessarily the optimum. the algorithm uses two lists, called opened and closed. Opened list contains the nodes that are possible to be selected and the closed contains the nodes that have already been selected. Firstly, the algorithm calculates the heuristic value of the first node, using the manhattan distance, and appends that node to the opened list (initialization phase). After that, remove the initial node from the opened list put it on the closed list, and, calculate the heuristic value of its children. For its child, if the child does not in both lists, or is in the opened list but with a bigger heuristic value, then the corresponding child is appended to the opened list in the position of the corresponding node with the higher heuristic value. In each step, the node with the minimum heuristic value is selected and removed from the opened list. The whole process is terminated when a solution is found, or the opened list is empty, meaning that there is no possible solution to the related problem. The pseudocode of the Greedy algorithm is the following:
1. function Greedy(Graph, start, target):
2. calculate the heurisitc value h(v) of starting node
3. add the node to the opened list
4. while True:
5. if opened is empty:
6. break ### No solution found
7. selecte_node = remove from opened list, the node with
8. the minimun heuristic value
9. if selected_node == target:
10. calculate path
11. return path
12. add selected_node to closed list
13. new_nodes = get the children of selected_node
14. if the selected node has children:
15. for each child in children:
16. calculate the heuristic value of child
17. if child not in closed and opened lists:
18. child.parent = selected_node
19. add the child to opened list
20. else if child in opened list:
21. if the heuristic values of child is lower than
22. the corresponding node in opened list:
23. child.parent = selected_node
24. add the child to opened list
Pen and Paper Example
Before proceeding with the implementation in Python, let’s see an example to better understand the whole algorithmic procedure. In this example, we are going to use a maze as follows:
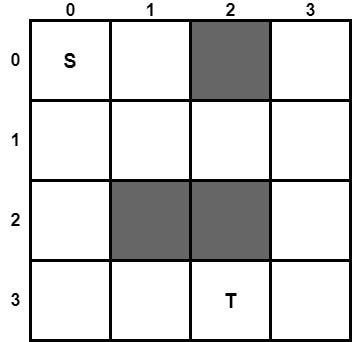
Suppose we have a robot and we want the robot to navigate from point S in position (0, 0) to point T in position (3, 2). The grey squares are obstacles that cannot pass the robot. To find a path from point A to point T, we will use the Greedy Algorithm. As a heuristic function, we will use the Manhattan Distance. Thus, we are going to calculate the Manhattan Distance of all the cells of the maze, using the formula above. For example, the Manhattan distance for the starting point is calculated as follows:
manhattan((0, 0), (3, 2)) = |0–3| + |0–2|= 3+2 = 5
The value five corresponds to the minimum path from point S to T and you can image it as following:

Remember that the heuristic value must be lower or equal to the real distance between the two points. Manhattan distance in a maze problem satisfies this restriction. Subsequently, the manhattan distance between each position with the final position is the following:
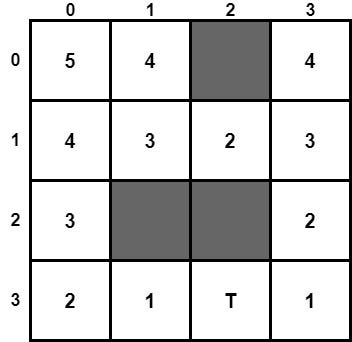
As we already know, we can model the above maze in the following graph:

Graph Data Structure — Theory and Python Implementation
Now we are ready to execute the Greedy algorithm to find a path from node S to node T.
Step 1: Initialization
We calculate the heuristic value of node S and put it on the opened list.

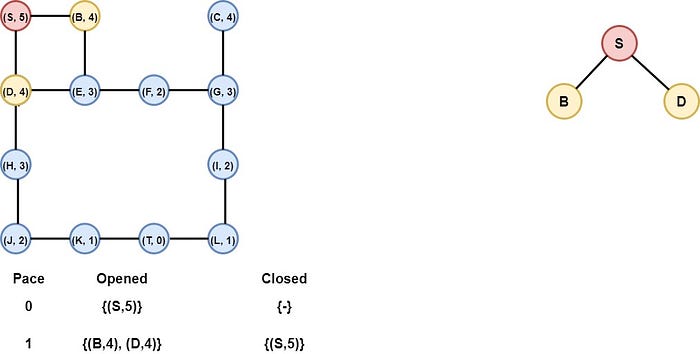
Step 2: Node S is selected
Node S is removed from the opened list and is added to the closed list. At the same time, the children of S, nodes B, and D are added to the opened list.
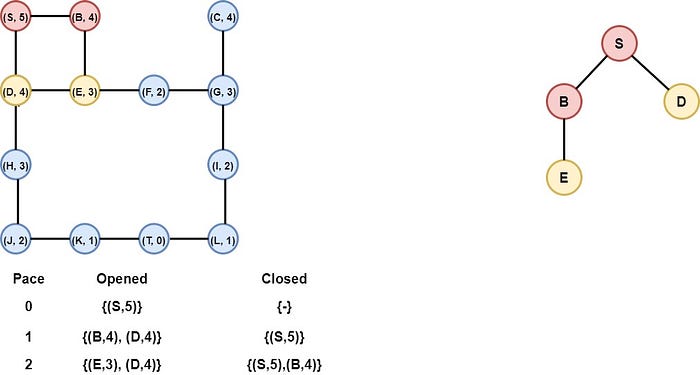
Step 3: Node B is selected
Nodes B and D have the same heuristic value. We choose node B arbitrarily. Node B goes to the closed list and its child, node E is inserted into the opened list. Notice that node B has as a neighbor node S, but S is already in the closed list, we do not insert it on the opened list.
Step 4: Node E is selected
Node E is selected as it has the smallest heuristic value. So it is inserted into the closed list, and its child, node F, is inserted into the opened list. The other child of E, node D is already in the opened list with the same heuristic value, so we do not insert it again in the opened list.

Step 5: Node F is selected
Node F is selected as it has the smallest heuristic value. The node is inserted into the closed list and its child, the node G, is inserted into the opened list.
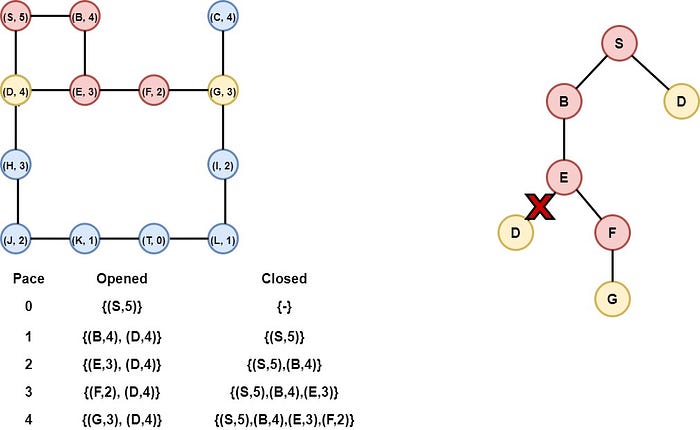
Step 6: Node G is selected
Node G is selected as it has the smallest heuristic value and is inserted into the closed list. Its children, nodes I and C are inserted into the opened list.

Step 7: Node I is selected
Node I is selected and inserted into the closed list. The child of node I, node L is inserted into the opened list.

Step 8: Node L is selected
Node L is selected and inserted into the closed list. Its child, node T is inserted into the opened list.

Step 9: Node T is selected
Node T is selected as it has the smallest heuristic value (zero). Node T is our target, so the algorithm stops the iteration and returns the path from S to T. The final path is S-B-E-F-G-I-L-T.
Python implementation
Understanding the whole algorithmic procedure of the Greedy algorithm is time to deep dive into the code and try to implement it in Python. We are going to extend the code from the Graphs article.
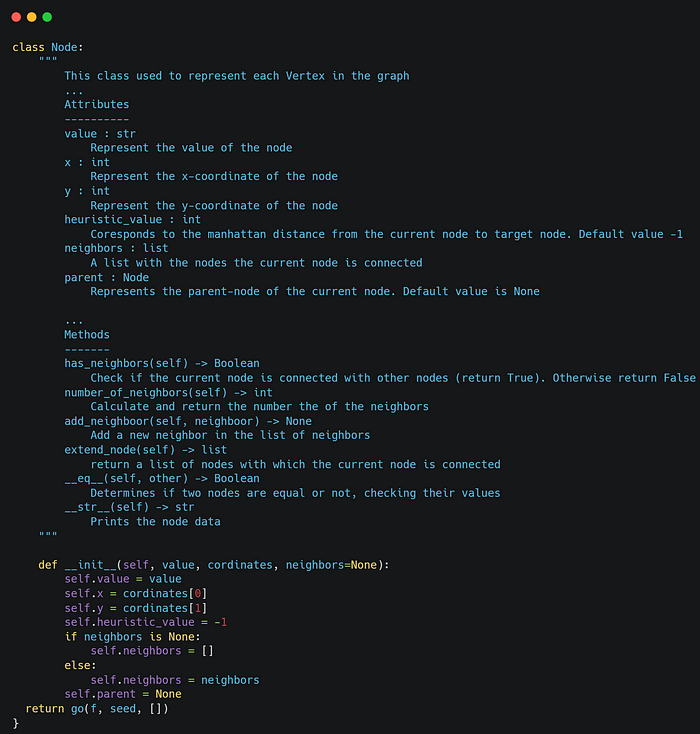
Firstly, we create the class Node to represent each node (vertex) in the graph. The node has various attributes such as the value, the coordinated x, and y, the heuristic value, etc. An overview of the Node class is the following.
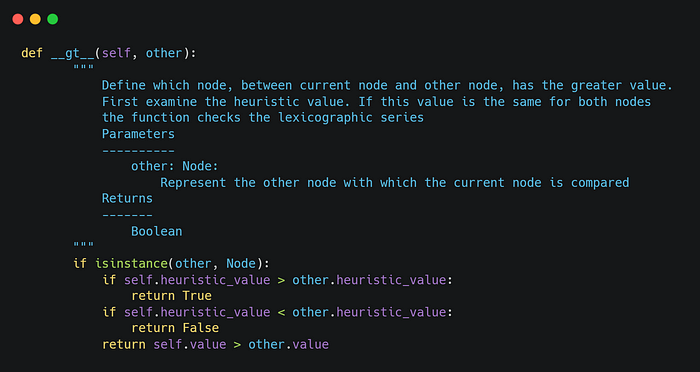
To compare the nodes we implement the magic or dunder method _gt()_. This method defines the way the nodes are compared whenever we sort the opened list. In this example, we are interested in the heuristic value. So we compare the nodes based on their heuristic values.
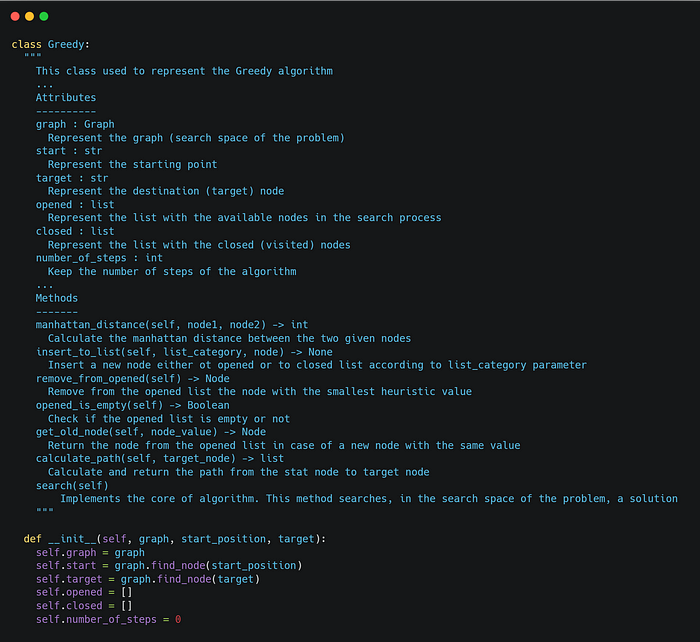
After that, we implement the class Greedy, which represents the algorithm. The class Greedy has a couple of attributes, such as the graph (search space of the problem), the starting point, the target point, the opened and closed list, etc. An overview of the class is the following:
Learn How to Use the gt() Method in Python
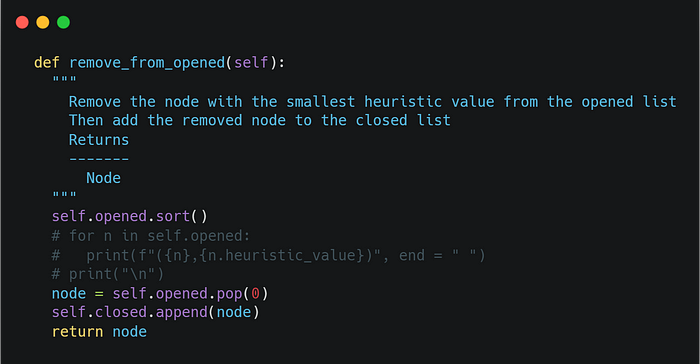
To calculate the manhattan distance we create the following function
Finally, the core algorithm is the following
Example
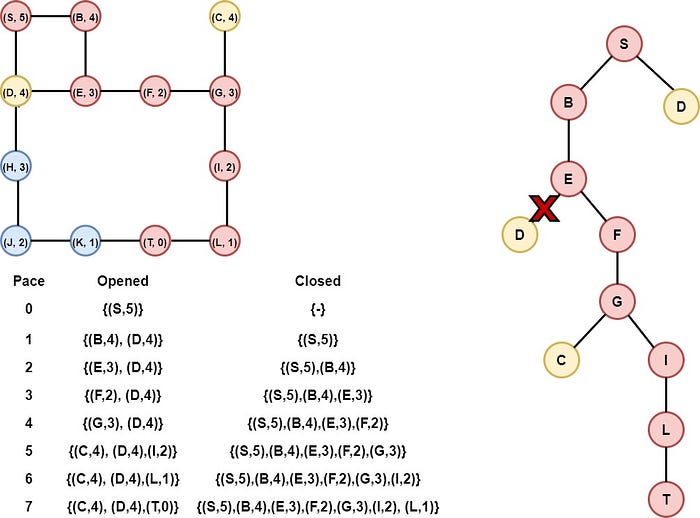
Now, we have the algorithm and we are able to execute the Greedy algorithm in any graph problem. We are going to check the algorithm in the example above. The graph is the following:

So we will model the above graph as follows and we will execute the algorithm.

We can notice that we got the same results. Be careful, in some cases, the Greedy algorithm may return the optimal solution by chance. The rule is that the Greedy algorithm doesn't return always the optimal solution.
You can see and download the whole code here.
Conclusion
In this article, we had the opportunity to talk about the Greedy algorithm, to find a path from the initial node to the target node. In contrast to other search algorithms we have seen so far such as DFS and BFS, the Greedy algorithm is a heuristic algorithm, that uses various heuristic methods to find a solution to a given problem. However, it doesn't always return the optimal solution. In the future, we will have the opportunity to talk about other heuristic search algorithms, such as the UCS and the A* algorithm. Until then, keep learning and keep coding. Thanks for reading.
If you like reading my articles follow me on LinkedIn and Twitter.
Comments
Loading comments…