Analytical Differentiation using Sympy in Python

Introduction

Differential calculus studies the rates at which quantities change.

This article demonstrates how to evaluate nth order symbolic derivatives in Python using the SymPy library.

Review this article to understand the fundamentals of differentiation, numerical differentiation, and a basic implementation of Euler’s method in Python using NumPy before working through the following content.

How is Numerical Differentiation Done Using Python

Theory

Equation 1 is an arbitrary sample function f(t), which will be used to demonstrate symbolic differentiation in Python.

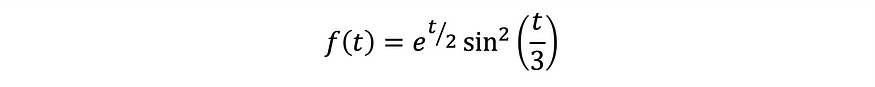
Working out the fourth derivative of Equation 1 is non-trivial. It requires knowledge of multiple rules of differential calculus.

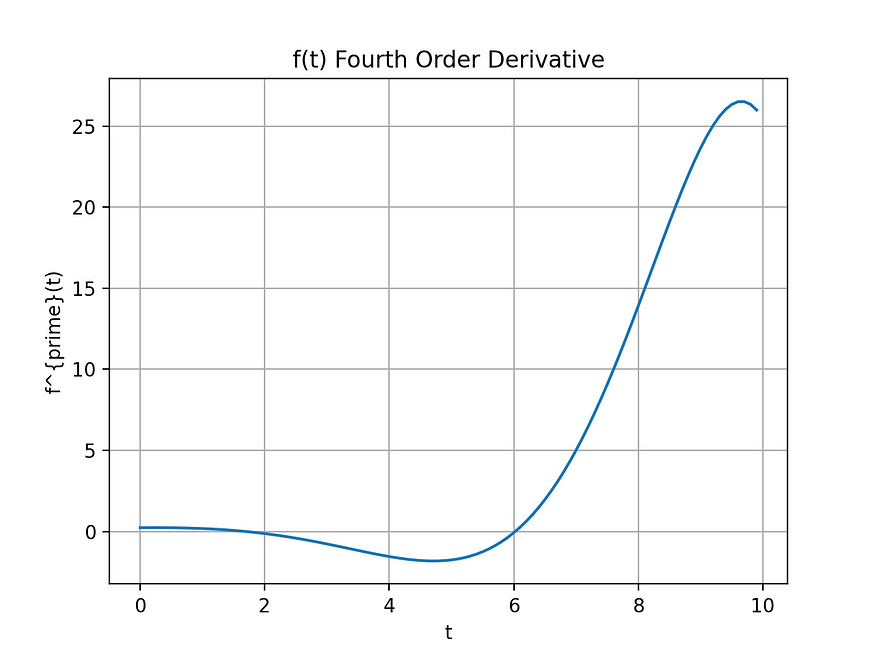
Wolfram Alpha is an invaluable resource for mathematics. Equation 2 is the solution to the fourth derivative of f(t), found by using the tool.

SymPy is an open-source Python library for symbolic computation.

Symbolic mathematics programs apply differentiation rules to find an analytical solution of the derivative of a function. This method is different from numerical differentiation, which is finding the numerical value of a derivative of a function at a given point.

Python Implementation

Obtaining the derivative in Equation 2 using the SymPy library is straightforward, as shown in Gist 1.

# import library
import sympy as sp

# define symbolic variable
t = sp.symbols('t')

# define symbolic equation
eq = sp.exp(t / 2) * (sp.sin(t / 3) ** 2)

# find fourth order derivative
fourth_order_derivative = eq.diff(t, t, t, t)

Indicated by the comments in the code above, the four essential steps are:

• Import the SymPy library
• Define the symbolic variable
• Create the symbolic equation. Precede specific terms with sp to access the SymPy declarations.
• Find the nth order derivative using eq.diff(…). The number of t’s supplied to the diff function is the order of the resulting derivative.

Executing this code and printing the fourth-order derivative yields the output in Figure 1, the same result obtained using Wolfram Alpha.

Thus, SymPy makes it trivial to calculate higher-order symbolic derivatives. Furthermore, numerically evaluating the result involves solving a substitution problem. Gist 2 gives the Python code for the substitution operation.

# define analysis time range
start = 0
stop = 10
time = np.arange(start, stop, 0.1)

# fourth-order numerical evaluation using substitution
numerical_solution = [fourth_order_derivative.subs({t: point}) for point in time]

# plot derivative time history
ax.plot(time, numerical_solution)

Plotting the numerical solution gives Figure 2.

As shown, SymPy offers an adequate set of methods to find an analytical equation for nth order derivatives of f(t).

An additional practical step in the procedure is to store the list of intermediate derivative functions. Maintaining this list can be achieved easily in Python, and the implementation shown in Gist 3 is one such recursive solution.

def differentiate(func, order, derivatives=None):
    """
    recursively find symbolic derivatives
    func: symbolic function to differentiate
    order: highest order derivative (interger)
    derivatives: func, intermediate derivative, nth order dt
    """

    # initialize list of derivatives
    if derivatives is None:
        derivatives = [func]

    # check if highest order derivative is reached
    if len(derivatives) > order:
        # return list of derivatives
        return derivatives

    # differentiate function
    derivative = func.diff(t)

    # append to list of symbolic derivatives
    derivatives.append(derivative)

    # recursive call to find next derivative
    return differentiate(derivative, order, derivatives)

The general steps in the process are outlined below.

1. On the first call to the recursive method, func equals the symbolic version of the known function f(t).
2. Each subsequent recursive parameterisation uses the most recent symbolically evaluated derivative, i.e. func is updated with f’(t) on the first pass and updated with f’’(t) on the second pass.
3. The recursion continues until the derivatives list length exceeds the specified order.

Results

Calling the function above parameterised with Equation 1, specifying the order as four, generates the list of function derivatives, shown in Figures 3 and 4.

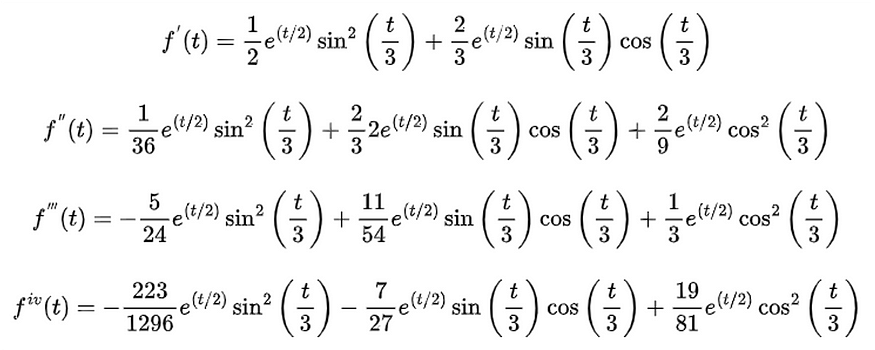
Note that the equation for the fourth derivative appears different than Equation 2; however, they are equivalent. Plotting both prove that they are the same function in two other representations.

Substituting values of t over the range 0–10 and plotting in Matplotlib gives Figure 5.

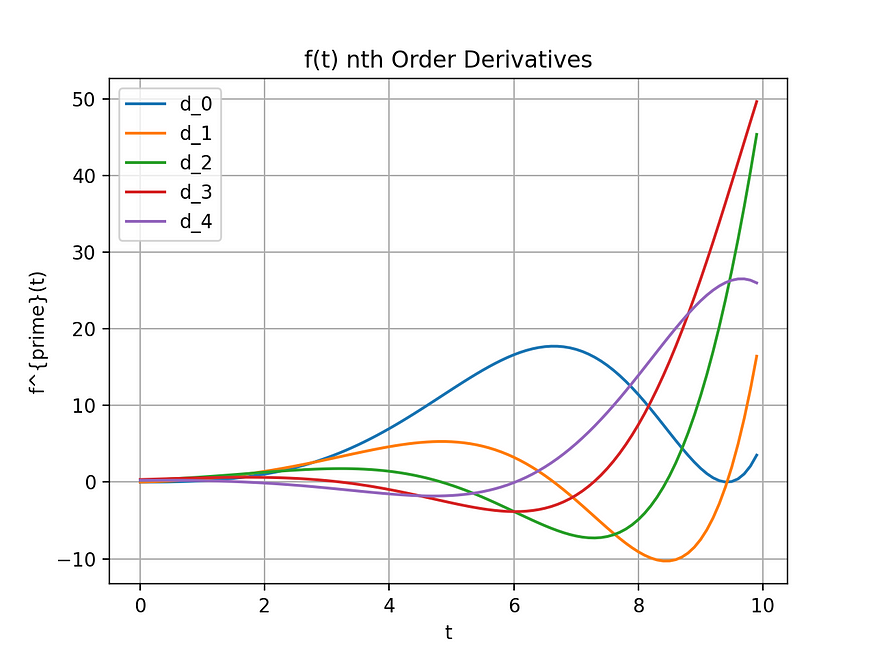
This Figure is comparable to the one obtained in the numerical differentiation article describing Euler’s method. However, this solution generates higher accuracy results.

Conclusion

In summary, this article has demonstrated how to evaluate nth order derivatives in Python using SymPy symbolically.

Understanding the operation is helpful for various applications in maths, science, and engineering. One such application involves finding a Taylor Polynomial, a polynomial used to approximate a function around a specific point a.

• How to Approximate a Function using Taylor Polynomials in Python

Check out my other articles if you’re interested in engineering, data science and Python programming. Thank you for reading.

• Join Medium with my referral link - Andrew Joseph Davies
• 5 Python Projects for Engineering Students