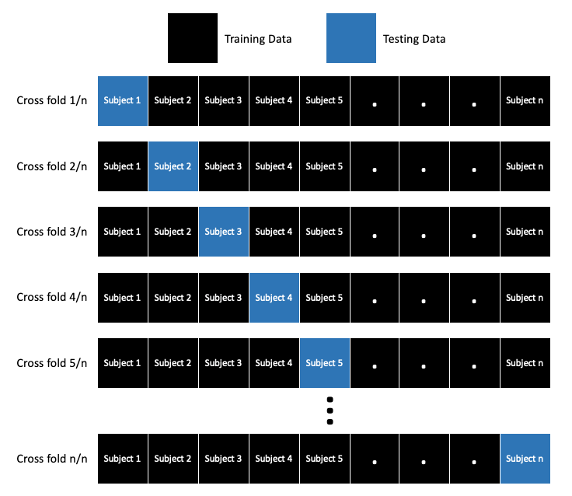
Leave one subject out cross validation approach. Image by the author.
Introduction
Cross validation is a technique used for training and testing machine learning models. When fitting a machine learning model using cross validation, the model is trained on a subset of data points and tested with the remaining data. This is repeated n times, where n is equivalent to the number of cross folds.
One approach is to use leave one out cross validation (LOOCV), where n is equal to the number of observations in the dataset. LOOCV trains the model on n-1 samples (or observations) and tests on the sample that was left out of training (hence the name). This technique is appropriate for small datasets and when model accuracy is more important than computational cost.
Datasets for human subject research can be small, especially when working with human movement data from optical motion capture or wearable sensors. Because of this, LOOCV is an applicable technique for building accurate models.
Instead of leaving out one sample, a common approach is to use leave one subject out cross validation, where all observations from a single subject are left out of the training dataset (also referred to as leave one person out cross validation).
This post will discuss why leave one subject out cross validation is an important tool for analyzing data collected on human subjects and show how I implement it in Python from scratch. By the end of this post, you will be able to use this approach to increase the accuracy of your predictive models.
💡 As an aside, if you’re interested in building Azure ML Pipelines using Python, check out this guide:
Building Azure Machine Learning Pipelines Using Python
Example Dataset
Let’s start with a sample dataset: data recorded from inertial measurement units fastened to the right limb of people while they are walking. Each subject (20 total subjects) wore an inertial measurement unit (IMU) while they walked at three different speeds — slow, comfortable, and fast for 6 trials total at each speed.
Within each trial, each subject took 20 strides. We would like to classify their gait speed using the signals from the inertial measurement unit. For the purposes of this explanation, I assume that all of the subjects took the same number of strides per trial of data collection, although that is not typically the case.
Sample dataset:

20 strides per trial at 6 total trials is 120 trials per subject per speed. Since each subject completed all 6 trials at 3 walking speeds, the total number of observations per subject is 120 _ 3 = 360. With 20 participants in the study, the total number of observations is 360 _ 20 = 7200. The features of this dataset are the angular velocity signals from the IMUs. The IMU sensor records 3 planes of motion (equivalent to 3 total angular velocity signals).
Each signal is 100 data points, so we end up with 100 * 3 = 300 total features in our dataset. Thus, the final data matrix is 7200 rows and 300 total columns, where each row is a single stride and each column is a data point of the angular velocity signal.
Sample data matrix (7200 rows and 300 features):

Why leave one subject out, and not just a single observation?
Using LOOCV would leave you with 7199 observations in each cross fold (the left-out sample would be the test dataset). Why is there a problem with this? Well, that training dataset of 7199 observations has strides from the subject that is the single test sample.
Since we are talking about movement data, that left-out stride is going to look pretty similar to most of the other strides that are a part of the training set. Therefore, the angular velocity signal is going to look very similar as well.
The problem is that this approach is testing the model using a sample that is very similar to some of the data in the training set. If this model is deployed or used for future predictions, the model will most likely not perform well if it has not seen features that are similar to the training data. In other words, the model was overfitted.
Instead of leaving out a single observation, an alternative approach is to leave out all observations from a single subject or person. In this dataset, the model would be trained on 6840 samples and tested in the remaining 360. This approach is great because you are maximizing the number of folds when cross validating the model, but the model is not being trained and tested on data from the same person.
Pneumonia Classification — An Alternative Example
X-ray of a patient with pneumonia. Image credit: Mayo Clinic

Back in 2017, a team led by Andrew Ng published a paper where they used frontal view x-ray images (112,120 total images) from 30,805 unique patients to train a deep learning model to classify if the patient did or did not have pneumonia (see latest publication here). In the first version of this publication, the team reported that the dataset was randomly split (80% training and 20% testing). Notice the ratio of images to patients? They had almost 4 times more images than patients. When randomly splitting the dataset, it is highly probable that images from the same individual landed in both the training and testing set, which is not optimal for validating your model.
Excerpt from the original article. Credit to Rajpurkar et al. 2017:
Fortunately, the team caught and corrected the mistake by randomly splitting the training and testing data by patient, not by image. They re-released the paper with the correct split.
Excerpt from the updated article. Credit to Rajpurkar et al. 2017
The difference with their dataset, which allowed them to split it into 80% training and 20% testing is the high sample size. Collecting this many images would take a long time, and would be an even longer process if it was human movement data instead of images. However, it is similar to the leave one subject out cross validation approach because the same patients were not included in both the training and testing set. Big thanks to Santiago Valdarrama’s twitter for this real-world case.
I hope that this example reinforces the importance of ensuring that subjects or patients are not included in both training and testing data. Next up, we’ll work through how to implement this from scratch with a dataset using IMU signal data.
Implementation in Python
Scikit-learn’s GroupKFold and StratifiedGroupKFold make it easy to implement leave one subject out cross validation. Check out the documentation for more info. When learning about these concepts, it is also beneficial to walk through implementing them from scratch. This can be done using some simple pandas functions and a for loop. Let's get started.
Sample Dataset
This data was constructed from an open-source dataset from Miraldo et al. of people walking at 3 different speeds with multiple wearable sensors. The open-source dataset contains 6 trials at each speed. The subjects wore 2 IMUs on the right leg (one on the lateral side and one on the medial side). There are 6 signals in total (3 angular velocities * 2 IMUs = 6 signals) that were individually resampled to 101 time points for a total of 606 features. Accounting for all strides resulted in 12,102 total strides. Therefore, the data matrix has 12,102 rows and 600 features. There are also columns for the ID of the subject (subject_ID), speed, and trial number. I also had to standardize (z-transform) the signals so they are all within the same numerical scale. If you are interested in how I restructured the data to this format, see the project on my GitHub.
First, import the libraries and load the data as a pandas DataFrame.
#import libraries
import os
import numpy as np
import pandas as pd
#import machine learning libraries
#pre-processing
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import StandardScaler
#import evaluation metrics
from sklearn.metrics import accuracy_score
#deep learning
# gather software versions
import tensorflow as tf
import keras
#scikit learn
from sklearn.utils import shuffle
from sklearn.utils import class_weight
#deep learning
from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation, Flatten
from keras.layers import Convolution1D, Conv1D, MaxPooling1D, GlobalAveragePooling1D
from tensorflow.keras.utils import to_categorical
from tensorflow.keras.optimizers import Adam
#plotting
import matplotlib.pyplot as plt
%matplotlib inline
%pylab inline
%config InlineBackend.figure_format = 'retina'
#ignoring warnings
import warnings
warnings.filterwarnings("ignore")
#import data
data = pd.read_csv(os.getcwd()+'/strides/ML_data/R_variables_all_std.csv', sep=',', index_col=0)
data
Pandas dataframe:

Next, I made a deep-learning model with 1D convolutional layers using keras.
#deep learning architecture
model = Sequential()
#since we only have a 1D vector, only 1D convolutional layers are needed
model.add(Conv1D(filters=16, kernel_size=2, input_shape=(101, 6)))
model.add(MaxPooling1D(pool_size=2))
model.add(Conv1D(filters=32, kernel_size=2, activation='relu'))
model.add(MaxPooling1D(pool_size=2))
model.add(Dropout(0.3))
model.add(Conv1D(filters=64, kernel_size=2, activation='relu'))
model.add(MaxPooling1D(pool_size=2))
model.add(Dropout(0.3))
model.add(GlobalAveragePooling1D())
model.add(Dense(64, activation='relu'))
model.add(Dense(32, activation='relu'))
model.add(Dense(len(encoder.classes_), activation='softmax'))
model.summary()
Compile the model
#compile model
model.compile(loss='categorical_crossentropy', metrics=['accuracy'], optimizer=Adam(lr = 0.001))
Now that the model is built, leave one subject out cross validation can be used to train and test on each cross fold. Since there are 22 subjects, there will be 22 cross folds in this process. First, create a list of all of the unique subject IDs.
#get a list of all subjects
all_subjects = data['subject_ID'].unique()
Also, create an empty list to store accuracy scores in. To evaluate the model’s performance with cross validation, the accuracy is calculated for each cross fold and and the average accuracy over all cross folds is calculated as a representative performance measurement.
#create an empty list to store accuracy in
accuracy_list = []
Next, iterate over all subject IDs in the all_subjects list and follow this procedure:
- For each iteration, select only the observations containing the subject ID as the test dataset, and select all other observations as the training set. The labels for the test/train split are selected in the same way. For the data, the subject_ID, speed, and trial must be dropped.
- Convert the training and testing data to arrays and reshape them
- Encode the labels into machine-readable form
- Fit the model and calculate the max accuracy over all epochs. Mean accuracy over all epochs could also be used to evaluate performance.
- Store the accuracy in the empty list created above
#loop over all conditions
for idx, subject_ID in enumerate(all_subjects):
#1) assign testing and training data
x_train = data.loc[data['subject_ID'] != subject_ID].drop(['subject_ID', 'speed', 'trial'], axis=1)
x_test = data.loc[data['subject_ID'] == subject_ID].drop(['subject_ID', 'trial', 'speed'], axis=1)
y_train = data.loc[data['subject_ID'] != subject_ID]['speed']
y_test = data.loc[data['subject_ID'] == subject_ID]['speed']
#2) convert training and testing data to arrays and reshape into (num_of_examples, num_of_features, num_of_signals)
X_train = np.asarray(x_train)
X_train = X_train.reshape(X_train.shape[0], 101, 6)
X_test = np.asarray(x_test)
X_test = X_test.reshape(X_test.shape[0], 101, 6)
#3) encode training and testing labels (switch from letters to one hot encoding)
encoder = LabelEncoder()
encoder.fit(y_train.values)
y_train = encoder.transform(y_train.values)
y_test = encoder.transform(y_test.values)
#Convert y_train and y_test to categorical variables
y_train = to_categorical(y_train)
y_test = to_categorical(y_test)
#4) fit model
history = model.fit(X_train, y_train, batch_size=64, epochs=2, validation_data=(X_test, y_test), shuffle=True)
#append max accuracy over all epochs
accuracy_list.append(max(history.history['val_accuracy']))
#get average of accuracies over all cross folds
mean_accuracy = mean(accuracy_list)
print('Average Accuracy: ', mean_accuracy)
That is the leave one subject out cross validation procedure that I implemented from scratch. It is based on iterating over a list of all subject IDs, selecting a subset of the original data, fitting the model, and repeating. If you are interested in the initial exploratory analysis of this dataset, feature reduction approaches, and how I landed on a deep learning model, check out the project on my GitHub.
Conclusion
Leave one subject/person out cross validation is a great approach for training and testing machine learning models to maximize accuracy with a small sample size. It is easy to implement from scratch or using python libraries. I hope this helps with implementing this process for your own projects. As always, feel free to reach out to me with any questions (rbrancati@umass.edu). I’m always open to chatting about data science, human performance, biomechanics, or other interesting areas.
References
Rajpurkar, P., Irvin, J., Zhu, K., Yang, B., Mehta, H., Duan, T., … & Ng, A. Y. (2017). Chexnet: Radiologist-level pneumonia detection on chest x-rays with deep learning. arXiv preprint arXiv:1711.05225.
Miraldo, Desiree; Watanabe, Renato Naville; Duarte, Marcos (2019): Dataset of gait and inertial sensors. figshare. Dataset. https://doi.org/10.6084/m9.figshare.7778255.v3
Comments
Loading comments…