The Most Expensive Peace Army

In the realm of chess, where queens, rooks, bishops, knights, and kings reign supreme, the conventional wisdom dictates specific numerical limits to their harmony on the board. But what if we shattered these constraints and melded their powers? Picture this: a chess army where queens, rooks, bishops, knights, and kings converge, each contributing a fraction of their might to a grander strategy. It's a challenge of strategic ingenuity, as we navigate the chessboard to orchestrate the most formidable force imaginable, where every piece coexists in perfect equilibrium, free from the threat of one another.

Let's attribute fractional values: 1/8 for a queen (Q), 1/8 for a rook (R), 1/14 for a bishop (B), 1/32 for a knight (N), and 1/16 for a king (K). Now, let's strategize to create the most valuable chess army possible on a chessboard, employing any combination of these pieces, while ensuring they coexist peacefully without posing a threat to one another.

Problem formulation:

before we formulate the problem we should start by the definition of neighbourhood for each chess piece

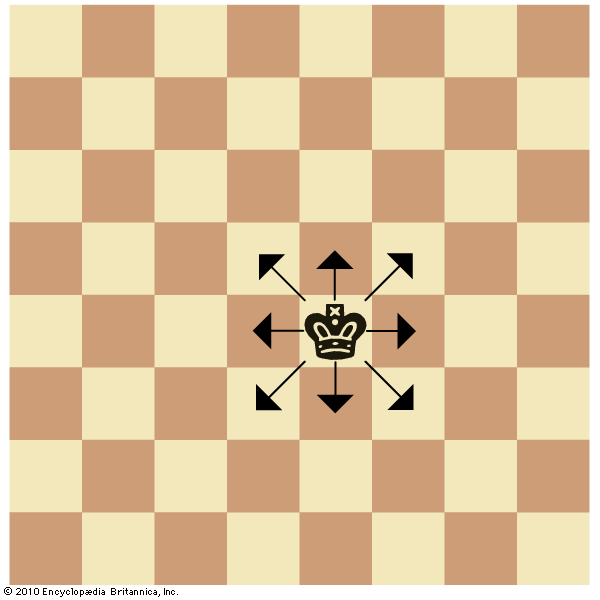
King

Any cell with a distance less than sqrt(2)

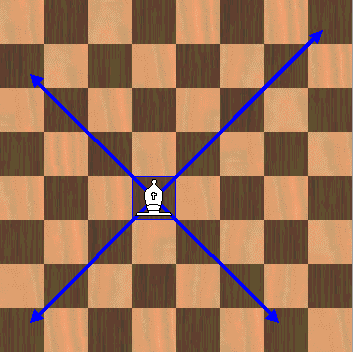
Queen

Let's find the neibours of cell i (x0,y0)

cell j is neghbour of cell i if it has any of these properties:

• X=x0
• Y=y0
• |X-x0|=|Y-y0|

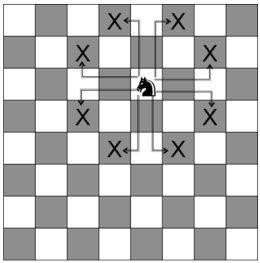
Knight

cell j is neghbour of cell i if it has any of these properties:

• (X-x0,Y-y0) in this list

[ (1,2),(1,-2) , (-1,2), (-1,-2) , (2,1), (2,-1) , (-2,-1),(-2,1) ]

Bishop

cell j is neghbour of cell i if it has any of these properties:

• |X-x0|=|Y-y0|

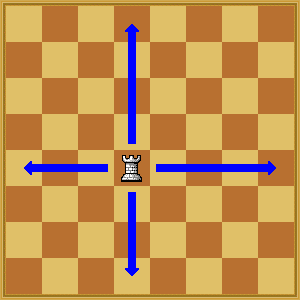
Rook

cell j is neghbour of cell i if it has any of these properties:

• X=x0
• Y=y0

Now let's talk about the math model:

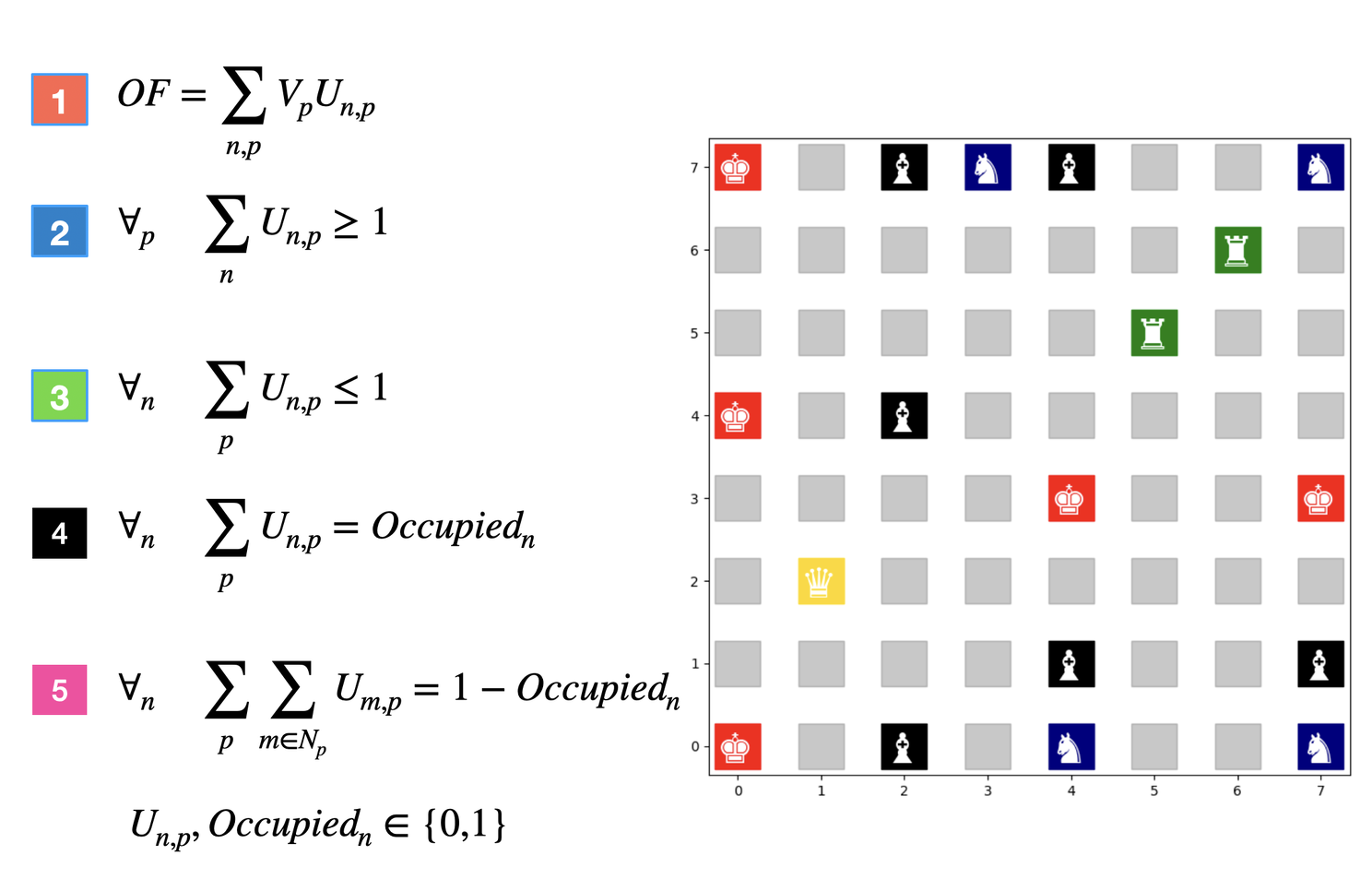
1. OF is trying to maximize the value of the army (Vp is the value of piece p)
2. For each piece (p): we need to have at least one cell assigned to it.
3. For each cell (n): not more than one piece can sit in it
4. if a piece is assigned to cell n then this cell is occupied
5. If a cell is occupied then there should be no other peice threatening this cell

def SolveWithTimeLimitSampleSat():
    model = cp_model.CpModel()
    # Creates the variables.
    pieces = ['K', 'R', 'Q', 'N', 'B' ]
    val= {'K':14, 'R':28, 'Q':28, 'N':7, 'B':16 }
    symb= {'K':"\u265A", 'R':"\u265C", 'Q':"\u265B", 'N':"\u265E", 'B':"\u265D" }
    U = {(n,p):model.NewBoolVar(f'assign_{n}_{p}') for n in nodes for p in pieces}
    Occupied = {n:model.NewBoolVar(f'O_{n}') for n in nodes}
    
    for p in pieces:
      expressions = [U[n,p] for n in nodes]
      model.AddAtLeastOne(expressions)

    for n in nodes:  
      expressions = [U[n,p] for p in pieces]
      model.Add(sum(expressions) == Occupied[n])
      model.AddAtMostOne(expressions)
      expressions_king_around   = [U[counter,'K'] for counter in nodes if counter in Nking[n] ]
      expressions_rook_around   = [U[counter,'R'] for counter in nodes if counter in NR[n] ]
      expressions_queen_around  = [U[counter,'Q'] for counter in nodes if counter in NQ[n] ]
      expressions_knight_around = [U[counter,'N'] for counter in nodes if counter in Nknight[n] ]
      expressions_bishop_around = [U[counter,'B'] for counter in nodes if counter in NB[n] ]
      
      around = expressions_king_around + expressions_rook_around + expressions_queen_around + expressions_knight_around + expressions_bishop_around
      model.Add( sum(around) == 0 ).OnlyEnforceIf(Occupied[n])

    expressions_of = [val[p]*v for (n,p),v in U.items() ]
    model.Maximize(sum(expressions_of))
    solver = cp_model.CpSolver()
    solver.parameters.max_time_in_seconds = 30.0
    status = solver.Solve(model)

    if status == cp_model.OPTIMAL or status == cp_model.FEASIBLE:
      print('OF = ', status, solver.ObjectiveValue())

Results :

Observations:

• The problem has symmetry and this makes it hard for solver to solve.
• There might be more than one solution
• The code is written using Constraint Programming Tool (ORTools) but the formulation is in MILP format.

Code on Github: https://github.com/OptimizationExpert/Pyomo