Covariance is the joint variability of two random variables, i.e. if the value of a variable x_ii increases how the value of x_ij changes. If the value of x_ii gets larger with the value of x_ij getting larger (and gets smaller together) we can say covariance is positive. If they move in opposite, then covariance is negative and if they are not correlation, covariance is 0 (zero).
For calculating covariance, we can use NumPy's covariance method:
import numpy as np
a = [[1,2,3],[6,7,8]]
c1 = np.cov(a)
print(c1)
>>
[[1. 1.]
[1. 1.]]
We can implement it without using NumPy or any external package in Python. First of all, we need to understand how to calculate covariance. The covariance of a matrix can be calculated using below formula (source: Wikipedia):
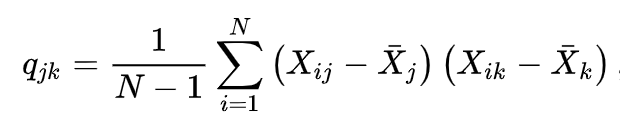
q_jk is the element in the covariance matrix (j-th row, k-th column). So basically, we calculate the mean of each column vector and sum the products of differences of column vectors from their mean.
To implement this, we first define a helper function to find individual q_jk covariance values given two column vectors of a matrix; i.e. v_j, v_k
def cov_value(x,y):
mean_x = sum(x) / float(len(x))
mean_y = sum(y) / float(len(y))
sub_x = [i - mean_x for i in x]
sub_y = [i - mean_y for i in y]
sum_value = sum([sub_y[i]*sub_x[i] for i in range(len(x))])
denom = float(len(x)-1)
cov = sum_value/denom
return cov
After defining our helper function, we are ready to calculate covariance values for each cell in the matrix. For this, our function will get a matrix as input and produce a covariance matrix:
def covariance(arr):
c = [[cov_value(a,b) for a in arr] for b in arr]
return c
This is it, we are done! Additionally, we can add a few extra controls to check whether the format and size of the input are correct. We can write a helper function like below to check vector lengths before calculating covariance matrix:
def check_vectors(arr):
length = len(arr[0])
x=[1 for a in arr if len(a)!=length]
if(sum(x)>0):
raise Exception(f'length of vectors not same')
The final code will look like below:
def cov_value(x,y):
mean_x = sum(x) / float(len(x))
mean_y = sum(y) / float(len(y))
sub_x = [i - mean_x for i in x]
sub_y = [i - mean_y for i in y]
sum_value = sum([sub_y[i]*sub_x[i] for i in range(len(x))])
denom = float(len(x)-1)
cov = sum_value/denom
return cov
def check_vectors(arr):
length = len(arr[0])
x=[1 for a in arr if len(a)!=length]
if(sum(x)>0):
raise Exception(f'length of vectors not same')
def covariance(arr):
check_vectors(arr)
c = [[cov_value(a,b) for a in arr] for b in arr]
return c