Solve Graph Coloring Problem with Greedy Algorithm and Python

Graph Coloring Problem is a classic problem in the Math field.

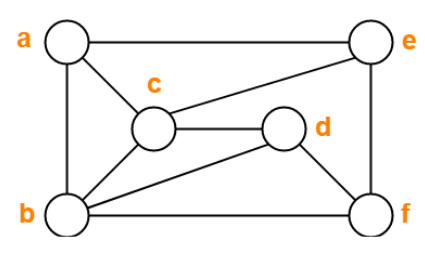
Let say we have a graph like in the picture above, and the problem is we must color each node with a different color for each adjacent node. We know that there is a theorem about this, the four color theorem, or the four color map theorem.

The four color theorem state that no more than four colors are required to color the regions of any map so that no two adjacent regions have the same color.

For more information about the four color theorem, you can look at this link:

Four color theorem - Wikipedia

The Greedy Coloring Algorithm

How the greedy coloring algorithm solves the problem, here is that algorithm:

• Initiate all the nodes.
• Set the node for the first coloring, the priority is the node with the largest degree.
• Choose the color candidate with the selection color function with no adjacent node having the same color.
• Check the eligibility of the color, if it's able to save to the solution set.
• Is the solution complete? Go to step 2 if not yet.

The Python Script

First of all, I have defined the color before.
Based on the four color theorem, I choose the 4 colors below:

Blue, Red, Yellow, Green

Step 1. Adjacent Matrix

Because we want to solve the problem with Python, we must represent the graph with the adjacent matrix. I'm not explaining about the adjacent matrix, you can find it at this link:

Adjacency matrix - Wikipedia

Here is the adjacent matrix from the graph above.

# adjacent matrix
G = [[ 0, 1, 1, 0, 1, 0],
     [ 1, 0, 1, 1, 0, 1],
     [ 1, 1, 0, 1, 1, 0],
     [ 0, 1, 1, 0, 0, 1],
     [ 1, 0, 1, 0, 0, 1],
     [ 0, 1, 0, 1, 1, 0]]

Then, we will initiate the name of the node with letters:

node = "abcdef"
t_={}
for i in range(len(G)):
  t_[node[i]] = i

Step 2. Count the degree and define the possible color

# count degree of all node.
degree =[]
for i in range(len(G)):
  degree.append(sum(G[i]))
# inisiate the posible color
colorDict = {}
for i in range(len(G)):
  colorDict[node[i]]=["Blue","Red","Yellow","Green"]

Step 3. Sort the node

I use selection sort for arranging the node from the largest to the lowest degrees.

# sort the node depends on the degree
sorted_node=[]
indeks = []# use selection sort
for i in range(len(degree)):
  _max = 0
  j = 0
  for j in range(len(degree)):
    if j not in indeks:
      if degree[j] > _max:
        _max = degree[j]
        idx = j
  indeks.append(idx)
  sorted_node.append(node[idx])

Step 4. The main process

This main process will look in the sortedNode and set the color with the possible colors in the colorDict and then save to theSolution. After that, that color will remove from colorDict because the color was used.

# The main process
theSolution={}
for n in sortedNode:
  setTheColor = colorDict[n]
  theSolution[n] = setTheColor[0]
  adjacentNode = G[t_[n]]
  for j in range(len(adjacentNode)):
    if adjacentNode[j]==1 and (setTheColor[0] in colorDict[node[j]]):
      colorDict[node[j]].remove(setTheColor[0])

Step 5. Print the solution

Print from theSolution Dict and sort them by the name of the node.

# Print the solution
for t,w in sorted(theSolution.items()):
  print("Node",t," = ",w)

Bonus Script

Let's make you lazy. Just copy and paste this script and run it.

# Adjacent Matrix

G = [[ 0, 1, 1, 0, 1, 0],
	 [ 1, 0, 1, 1, 0, 1],
	 [ 1, 1, 0, 1, 1, 0],
	 [ 0, 1, 1, 0, 0, 1],
	 [ 1, 0, 1, 0, 0, 1],
	 [ 0, 1, 0, 1, 1, 0]]

# inisiate the name of node.
node = "abcdef"
t_={}
for i in range(len(G)):
	t_[node[i]] = i

# count degree of all node.
degree =[]
for i in range(len(G)):
	degree.append(sum(G[i]))

# inisiate the posible color
colorDict = {}
for i in range(len(G)):
	colorDict[node[i]]=["Blue","Red","Yellow","Green"]

# sort the node depends on the degree
sortedNode=[]
indeks = []

# use selection sort
for i in range(len(degree)):
	_max = 0
	j = 0
	for j in range(len(degree)):
		if j not in indeks:
			if degree[j] > _max:
				_max = degree[j]
				idx = j
	indeks.append(idx)
	sortedNode.append(node[idx])

# The main process
theSolution={}
for n in sortedNode:
	setTheColor = colorDict[n]
	theSolution[n] = setTheColor[0]
	adjacentNode = G[t_[n]]
	for j in range(len(adjacentNode)):
		if adjacentNode[j]==1 and (setTheColor[0] in colorDict[node[j]]):
			colorDict[node[j]].remove(setTheColor[0])

# Print the solution
for t,w in sorted(theSolution.items()):
	print("Node",t," = ",w)

The Result

After running the script, here is the output:

If we represented again to graph, it will be like this:

Conclusion

You know that the solution just uses 3 colors. That's because our program will search for the minimum colors for coloring the graph. So with the graph before, we never meet the 4th color, because just with three colors we have the solution.

You can try another graph with this program, just replace the adjacent matrix and node = “abcdef” with yours.

If you learn something today, that's great, man. Thanks for reading.