Python's computer algebra system SymPy contains a submodule sympy.physics.units that is dedicated to handling physical units. I never worked with it before but I recently started to play with it a little bit. The documentation, though not really terse, is not very clear, unfortunately. At least to me. Here I give a quick overview of what I think is useful about this module, mostly unit conversion and dimensional analysis.
Converting Units
SymPy's unit system allows to easily convert quantities between different units of the same dimension, like converting lengths between meters and yards. The first step is always to define a Quantity, which is a number factor together with a unit. For instance, we can define a quantity of 5 meters as:
import sympy.physics.units as u
from sympy.physics.units.systems import SI
distance = u.Quantity('d')
SI.set_quantity_dimension(distance, u.length)
SI.set_quantity_scale_factor(distance, 5.*u.meter)
After defining distance as an abstract quantity, we then give it a dimension of lengths using the unit system of your choice (in this case SI unit system). You may wonder why we have to specify the dimension of some quantity through a specific unit system. Length is length, isn't it? Not always! Depending on what unit system you have, you have different relations between base dimensions.
For instance, in the SI unit system, like in many others, a velocity has dimensions "length / time". But in a natural unit system often used in relativity, the speed of light and thus all velocities are dimensionless numbers! And as a consequence, time and length have the same units. So in principle, the relation of a given dimension to the base dimensions of a specific unit system may be different. This is (probably) the reason for the design decision why you have to define the dimension of a quantity using a given unit system.
After defining the dimension, you define the factor. After that, the variable distance is a number 5 with units of meters.
Let's convert our distance to yards, so just call the convert_to function:
u.convert_to(distance, u.yards)
Out:
5.46806649168854yd
If you are unsure about the name of the unit in SymPy, you can use the find_unit function to search for it:
u.find_unit('mile')
Out:
['mile', 'miles', 'nautical_mile', 'nautical_miles']
Singulars and plurals can be used synonymously.
As another example, let's see how many Joules there are in one electron volt:
eV = u.Quantity('eV')
SI.set_quantity_dimension(eV, u.energy)
SI.set_quantity_scale_factor(eV, 1 * u.electronvolt)
u.convert_to(eV, u.joule)
Out:
1.602176634⋅10−19J1.602176634⋅10−19J
Dimensional Analysis
As an example for dimensional analysis, let's find out what dimensions the gravitational constant has. Newton's law of gravity reads

where 𝑚 and 𝑀 are masses, 𝑟 is the distance between the bodies, 𝐹 is the force between the bodies and 𝐺 is the gravitational constant.
from sympy.abc import *
newton = sympy.Eq(F, G * m * M / r**2)
Solve this equation for 𝐺:
G_ = sympy.solve(newton, G).pop()
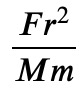
Here we have used pop because solve returns a list of solutions. But since there is only one solution for this linear equation, we can just pop the single entry from the list. Now that we have an expression for 𝐺, substitute the symbols by their respective dimensions:
dimG = G_.subs({F: u.force,
m: u.mass,
M: u.mass,
r: u.length})
What we want is the dependency of 𝐺 in terms of the base dimensions of our unit system. The function for that is a method of dimsys_SI which is an instance of the DimensionSystem class:
from sympy.physics.units.systems.si import dimsys_SI
dimsys_SI.get_dimensional_dependencies(dimG)
Out:
{'length': 3, 'mass': -1, 'time': -2}
The numbers in the dictionary are the exponents of the corresponding dimension.
Conclusion
SymPy's unit system allows to convert between different units and to analyze dimensions of expressions. Although this works quite well, the fact that its utility functions are more or less buried inside subsubsubmodules indicates for me that it is either rarely used or still heavily work in progress. Now it's no surprise to me that I didn't stumble upon it earlier. Nevertheless, it does its job.
Comments
Loading comments…