In the field of deep learning, Recurrent Neural Networks (RNNs) are extraordinary for handling sequences of data. Yet, lurking within their architecture is a puzzling challenge known as the vanishing gradient problem. In this article, we’ll demystify this issue, explaining why RNNs face it . I will avoid mathematical expressions to simplify for non technical people.

Recurrent Structure

• RNNs have a recurrent (looping) structure that allows them to process sequences of data one step at a time. At each step, they update their internal state and make predictions based on that state.

Gradient Computation

• During training, RNNs use gradient descent to adjust their parameters (weights and biases) to minimize the prediction error. This involves calculating gradients, which indicate how much each parameter should be adjusted to reduce the error.

Where:

• New Parameter Value is the updated value of the parameter.
• Old Parameter Value is the current value of the parameter.
• Learning Rate is a hyperparameter that controls the step size during the update.
• Gradient of Loss with respect to Parameter is the derivative of the loss function with respect to the specific parameter being updated.

Backpropagation Through Time (BPTT)

• RNNs use a technique called Backpropagation Through Time (BPTT) to compute these gradients. BPTT is a variant of the standard backpropagation algorithm, tailored for sequential data. It involves unrolling the RNN through time steps and calculating gradients step by step, from the end of the sequence back to the beginning.

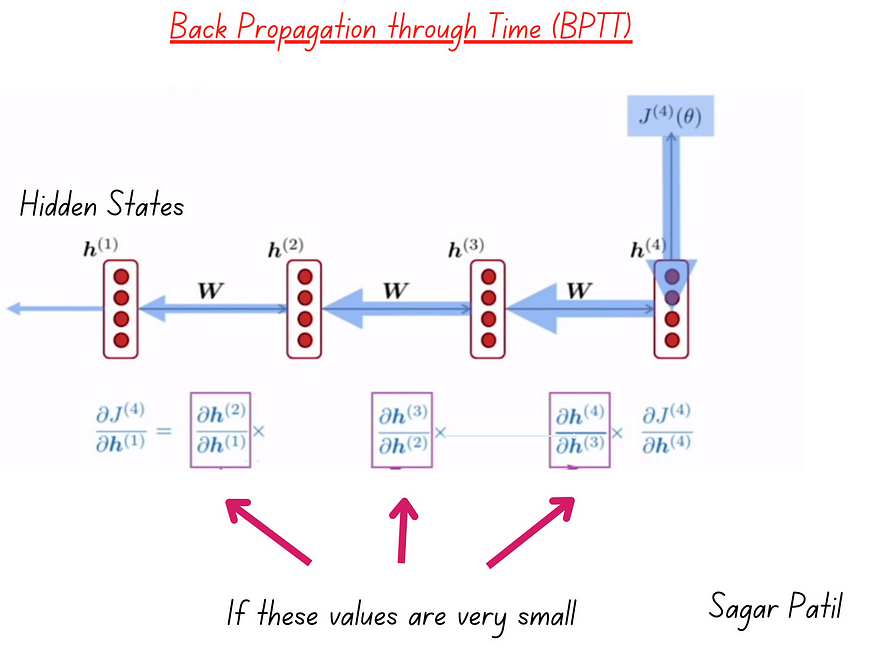
The Problem Emerges

• Now, here’s where the problem arises. As BPTT calculates gradients backward through time, it involves taking derivatives of the loss with respect to the model’s parameters at each time step. These derivatives are multiplied together as they are propagated backward.

Multiplicative Effect

• Since gradients are multiplied together, if the gradients at each time step are less than 1 (e.g., due to using activation functions like sigmoid or tanh that squash values between 0 and 1), this multiplication leads to a compounding effect. As you go further back in time, the gradients become increasingly smaller.

Vanishing Gradients

• The compounding effect causes the gradients for early time steps to become vanishingly small, approaching zero. When the gradients are too close to zero, they don’t provide meaningful information for parameter updates. This makes it challenging for the RNN to learn long-term dependencies in the data.

In summary, the vanishing gradient problem in RNNs occurs because gradients become extremely small as they are propagated backward through time during training, making it challenging for the network to effectively learn from distant past information in a sequence.

Impacts of vanishing gradients -

The vanishing gradient problem can have several significant impacts on the training and performance of neural networks:

Slow Convergence

• Training neural networks with vanishing gradients tends to be slow. Because gradients are very small, parameter updates are tiny, and it takes many iterations (epochs) for the model to converge to an acceptable solution. This extended training time can be computationally expensive.

Difficulty Learning Long-Term Dependencies

• The primary impact is that models affected by vanishing gradients struggle to capture and learn long-range dependencies in sequential data. In applications like natural language processing, speech recognition, or time series prediction, understanding context or patterns over a long sequence of data is crucial. The vanishing gradient problem makes it challenging for the model to retain information from distant past time steps, leading to poorer performance on tasks that require such memory.

Stuck in Local Minima

• The small gradients can sometimes cause the optimization process to get stuck in local minima. This means the model may not reach the best possible solution because it struggles to escape from regions of the loss function where the gradient is almost zero.

Model Instability

• Vanishing gradients can lead to model instability. Tiny perturbations in the input data or the model’s parameters can result in significantly different predictions, making the model less robust and reliable.

Overemphasis on Recent Data

• Models affected by the vanishing gradient problem tend to give more weight to recent data and neglect information from the past. This bias towards recent data can result in suboptimal predictions and a lack of historical context in the model’s outputs.

Difficulty in Training Deep Networks

• The vanishing gradient problem is more pronounced in deep neural networks with many layers. It becomes increasingly challenging to train deep networks, especially when standard activation functions like sigmoid or tanh are used, as they squash values between 0 and 1, making gradients even smaller.

Techniques to reduce vanishing gradient -

To reduce the vanishing gradient problem in Recurrent Neural Networks (RNNs), several techniques have been developed. Here is a list of some of these techniques, simplifi

Weight Initialization

• Initialize the weights of the RNN with carefully chosen values, like Xavier/Glorot initialization, to ensure that gradients are not too small initially.

Gradient Clipping

• Limit the size of gradients during training. If a gradient exceeds a certain threshold, scale it down to prevent it from becoming too small or exploding.

Use of Activation Functions

• Use activation functions that are less prone to vanishing gradients, like the ReLU (Rectified Linear Unit) or variants such as Leaky ReLU and Parametric ReLU (PReLU).

Skip Connections

• Implement skip connections or residual connections between layers of the RNN. This helps gradients flow more easily through the network.

Long Short-Term Memory (LSTM)

• Replace the standard RNN cells with LSTM cells, which are designed to better capture long-range dependencies and mitigate the vanishing gradient problem.

Gated Recurrent Unit (GRU):

• Similar to LSTM, GRU is another type of RNN cell that addresses the vanishing gradient problem by using gating mechanisms to control the flow of information.

Attention Mechanisms

• Integrate attention mechanisms into your RNN architecture. Attention mechanisms allow the network to focus on relevant parts of the input sequence, reducing the reliance on long-term dependencies.

These techniques aim to make it easier for gradients to flow through the RNN during training, preventing them from becoming too small and mitigating the vanishing gradient problem.