Algorithm challenges and I have been best friends lately. I say that not to brag, or to say I'm an expert quite yet, but just to say that I have a better understanding of them than I did last week. Looking back on my knowledge comparison, I have concluded as long as a developer steadily grows in any way they can, since the tech industry constantly brings new changes, then they are on the right track to keep themselves valuable to their teams or job marketplace if they are looking for a new role.
Besides shedding some light on this fact that constant learning is essential, for this week I wanted to go in greater detail to explain three different solutions explained for the most common algorithm question I keep seeing on every platform and every YouTube video; the ever-popular two-sum question. It seems like there are countless blogs written about how to solve it, some with clear explanations and some with not so clear explanations. Either way I wanted to explain my own take on it.
Big-O Explained
Before I get into the solutions, I wanted to take the time to briefly talk about Big-O notation and my understanding of it as it applies to the idea that some solutions are more efficient than others.
Big-O is basically a way to measure how efficient an algorithm runs in terms of how much space (memory) it takes up in a computer which is called space complexity and how fast it takes the algorithm to run, called time complexity, with both of these being relative to the size of the input of what goes into the algorithm in the beginning.
For instance let's say I have two algorithms and they both are supposed to take in arrays as the data structure and they both have to return a modified array in the end. If given the size of 5 elements as an input value to each, one will run faster than the other one, but still will ultimately produce the same results. We can say that the one that runs faster has better time complexity and to measure that we should choose a value from the Big-O notation options to put a label on that solution. Ultimately we would see that it runs more efficiently than the other algorithm because of what notation it receives.
A different way to look at this would be to say that Big-O notation to an algorithm is like a speedometer representing the speed acceleration of a car based on which kind of car you drive. If you drive a cherry red Ferrari, you'll get a faster Big-O than a worn out 1990s Honda Civic.
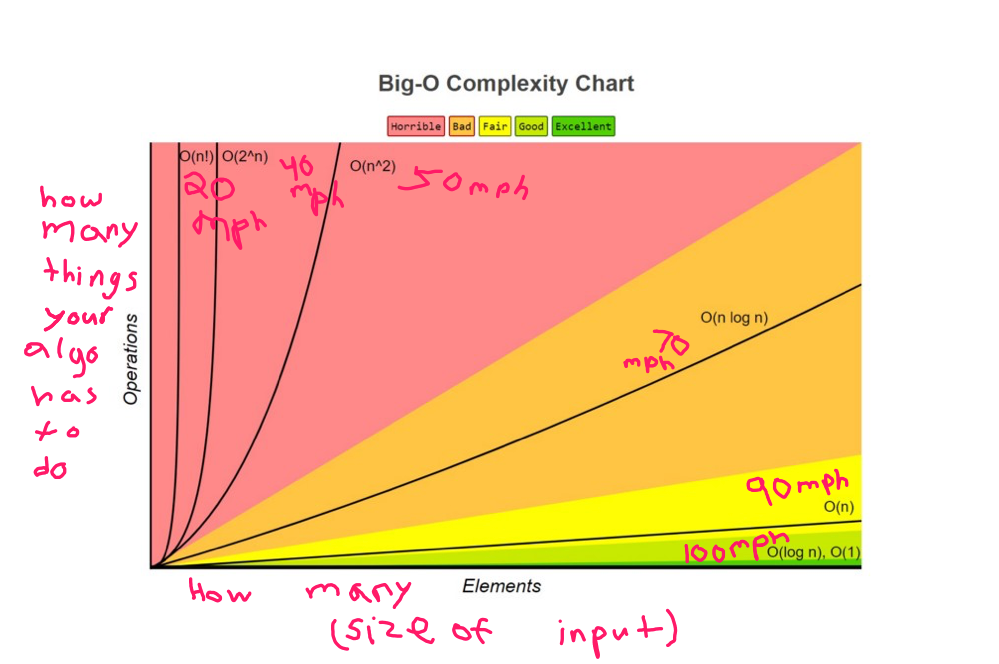A handy chart I've edited to simplify what it means to measure Big-O
I'll be adding the Big-O measurements for each of my solutions as I go through them as they are an important way to measure how efficient each of algorithms are. Also I should add, I will be coding my solutions in JavaScript.
The Problem
The two-sum problem is a question that asks that if given an array of integers (numbers), like [1, 2, 3], and a target sum number, such as 5, return an array of elements that add up to that target sum number. If no two numbers in the array add up to the target number, then we need to return an empty array; []. This comes with the restriction that you can't just add a single number to itself to make the sum.
Solution 1. Brute Force Method
Approach Summary: To start off the first solution I will give will be using two for loops to look through the numbers to check if they add up to the target number and then push the two numbers into an empty array and return that, otherwise if no two numbers add up, I'll return the original empty array.
How to solve: I've named my function below and given it the two appropriate arguments, the array given and the target number they should add up to be.
function twoNumberSum(array, targetSum) {
Next I've set up a variable called answer which will be assigned to an empty array and I've started a for loop which will start at the first element (that is why i is equal to 0) and keep on looking through the numbers one by one (i++) until it has looked through all the elements in the array (the condition in the middle; i < array.length).
function twoNumberSum(array, targetSum) {
let answer = []
for( i = 0; i < array.length ; i++){
Now I have started my second loop which will look at the number right next to whatever i represents the first time (j = i+1), each time increasing by one within the first loop (j++) until it looks through every number in the array (j<array.length). If the array given is [1, 2, 3], i would be 1 and j would be 2.
function twoNumberSum(array, targetSum) {
let answer = []
for( i = 0; i < array.length ; i++){
for( j = i+1; j<array.length; j++){
It is time to write the condition which is going to check if the first element; array[i] adds to the second element; array[j] to equal the target sum number. If it does then push the two numbers into the array. After pushing the elements in there, return the answer which was set to an array in the first place to hold our answer.
function twoNumberSum(array, targetSum) {
let answer = []
for( i = 0; i < array.length ; i++){
for( j = i+1; j<array.length; j++){
if(array[i]+array[j]===targetSum){
answer.push(array[i], array[j])
return answer
}
}
}
To end this off we need some way to return an empty answer array if we don't find two numbers that add up which is why we should add the last line here which says to return the array outside of the for loop.
function twoNumberSum(array, targetSum) {
let answer = []
for( i = 0; i < array.length ; i++){
for( j = i+1; j<array.length; j++){
if(array[i]+array[j]===targetSum){
answer.push(array[i], array[j])
return answer
}
}
}
return answer
}
The Big-O notation of this solution would be O(n^2) for time complexity and O(1) for space complexity, which indicates that it is not a very efficient solution for how fast it solves the problem.
Solution 2. Hash Method
Approach Summary: This solution ultimately makes a mini dictionary, which is a JavaScript object, that will place our numbers from our array into this dictionary. Then if the for loop finds the number from our dictionary which adds to the number we are on to be equal to the target sum, it will return both numbers as an array.
How to solve: For this solution I've started it off the same way as the first solution, this time adding a variable set equal to an empty JavaScript object or hash, an empty book for the time being.
function twoNumberSum(array, targetSum) {
let numbersObject = {}
Then we start our for of loop since we are looking through an array to check each element, not to be confused with for in loops that look through objects. Anyways the word number is a variable that represents each of our numbers in our array.
function twoNumberSum(array, targetSum) {
let numbersObject = {}
for (const number of array){
I am now going to set a variable called numberWeAreChecking assigned to our target sum minus the number we are on.
function twoNumberSum(array, targetSum) {
let numbersObject = {}
for (const number of array){
let numberWeAreChecking = targetSum — number
To write the condition that will check if the number we are checking exists in our object I have written the following. If it is found then that means it is the missing number to make the target sum, which is why we would return that number and the other number we were checking in the for of loop returned together in an array.
function twoNumberSum(array, targetSum) {
let numbersObject = {}
for (const number of array){
let numberWeAreChecking = targetSum — number
if ( numberWeAreChecking in numbersObject){
return [numberWeAreChecking, number]
Otherwise in all other cases we would want to add our number to our dictionary and assign it the value true. As the for of loop runs, our dictionary grows with each number inside set equal to true until it satisfies the numberWeAreChecking variable operation. To visually explain this concept better, each time the else statement runs the dictionary might go from looking like {} to {1:true, 2:true}, which means 1 and 2 both exist.
function twoNumberSum(array, targetSum) {
let numbersObject = {}
for (const number of array){
let numberWeAreChecking = targetSum — number
if ( numberWeAreChecking in numbersObject){
return [numberWeAreChecking, number]
}else{
numbersObject[number]=true
The for of loop stops running after it goes through all the numbers so once it finishes checking everything it will come out of the for loop which is why the next line returns an empty array. JavaScript functions stop running once they hit a return keyword and it would never hit a return keyword if the if condition isn't satisfied. So it would eventually hit the return keyword here after the for loop completes to return an empty array.
function twoNumberSum(array, targetSum) {
let numbersObject = {}
for (const number of array){
let numberWeAreChecking = targetSum — number
if ( numberWeAreChecking in numbersObject){
return [numberWeAreChecking, number]
}else{
numbersObject[number]=true
}
}
return [];
}
In terms of Big-O notation this solution has a notation of O(n) for time and O(n) for space. This means that it is better than the first solution in terms of speed, but not better than the first in terms of space as it takes extra space to store everything in the JavaScript object.
Solution 3. The Sort Method
Approach Summary: This solution is going to focus on sorting the numbers and using a left and right pointer system to eventually find the numbers to add up to the target sum. The right pointer is pointing to an integer and the left pointer is pointing to another integer in the array on each opposite side.
Each time while going through a loop to check each if each of these numbers add up to the target sum, the left or right pointer will move accordingly depending on if the sum of both numbers being pointed to is greater or smaller than the target sum.
How to solve: The solution starts off with being named and taking in the same inputs as the previous two solutions. Then uses the sort method to sort the numbers from least to greatest.
function twoNumberSum(array, targetSum) {
array.sort(function(a, b){return a-b})
There are three variables being defined here which will represent the indexes of the far left and far right side. All arrays start at the 0th index for the left side and whatever number counting backwards from the last number appears first represents the far right side. Then an empty array will again hold our answer if we don't find any two numbers that add up to the target which is represented by the word answer.
function twoNumberSum(array, targetSum) {
array.sort(function(a, b){return a-b})
let leftPointer = 0
let rightPointer = array.length-1
let answer = []
Now it is time to use a loop to look through each of our numbers starting from the beginning and to code an if condition that says if whatever number the left pointer is pointing to plus whatever number the right pointer is pointing to adds up to the target sum, then return these two numbers in an array.
function twoNumberSum(array, targetSum) {
array.sort(function(a, b){return a-b})
let leftPointer = 0
let rightPointer = array.length-1
let answer = []
for(i=0; i<array.length; i++){
if (array[leftPointer] + array[rightPointer]===targetSum){
return [array[leftPointer], array[rightPointer]]
If this condition is not satisfied, it means we haven't found our answer so the program will jump to the next else if statement which says that if the result of adding these numbers is smaller than the target sum move the left pointer closer to the right. Because these numbers are already sorted that will make our result next time the loop runs bigger which will bring it closer to the target sum number.
Otherwise the next else if condition will run which will do the opposite if it finds that the result is greater than the target sum number which will get the result closer to the target sum in the opposite direction.
function twoNumberSum(array, targetSum) {
array.sort(function(a, b){return a-b})
let leftPointer = 0
let rightPointer = array.length-1
let answer = []
for(i=0; i<array.length; i++){
if (array[leftPointer] + array[rightPointer]===targetSum){
return [array[leftPointer], array[rightPointer]]
} else if (array[leftPointer] + array[rightPointer] <targetSum) {
leftPointer++
} else if (array[leftPointer] + array[rightPointer] >targetSum){
rightPointer —
}
Closing things off, if the loop can't find the answer, it will return an empty array.
function twoNumberSum(array, targetSum) {
array.sort(function(a, b){return a-b})
let leftPointer = 0
let rightPointer = array.length-1
let answer = []
for(i=0; i<array.length; i++){
if (array[leftPointer] + array[rightPointer]===targetSum){
return [array[leftPointer], array[rightPointer]]
} else if (array[leftPointer] + array[rightPointer] <targetSum) {
leftPointer++
} else if (array[leftPointer] + array[rightPointer] >targetSum){
rightPointer —
}
}
return answer
}
The Big-O notation for this solution is going to end up being defined as O(nlog(n)) for time and O(1) for space which means that this solution was better than the second solution in terms of space, but worse than the second solution in terms of speed. However it is still better than the first solution in terms of time complexity.
The two sum problem in itself is a common algorithm question that I've seen everywhere online and commonly given during technical interviews which is why I figured it would be useful to explain how to solve it in the three ways I've described.
I hope this was useful to somebody trying to understand each method for solving this problem or trying to understand Big-O. If you haven't understood it yet, I would encourage you to keep trying to since understanding these concepts will benefit you in the long run.
In other words, for me this question served as a stepping stone for me to understand more complicated algorithm problems later on down the road since it lays down the basics of what algorithm solutions can look like. I'm committed to doing more and learning more to maintain consistent growth in the field of software development, which is something I also think every developer should also aspire to continue to do. With a better understanding of algorithms, we'll all be able to write our Big-O Ferrari functions in no time!
Comments
Loading comments…